
如图,抛物线y=ax2 +bx+c经过点A(-3,0)、C(0,4),点B在抛物线上,CB
∥X轴.且AB平分∠CAO.
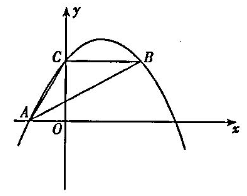
(1)求抛物线的解析式.
(2)线段AB上有一动点P,过P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,直接写出点M的坐标;如果不存在,说明理由,
解:(1)A(-3,0)、C(0,4),所以AC=5,OC=4.
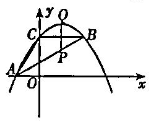
∵AB平分∠CAO ∴∠CAB=∠BAO
∵CB∥x轴∴∠CBA=∠BAO
∴∠CAB=∠CBA
∴AC=BC=5
∴B(5,4)………………………………………1分
A(-3,0)、C(0,4)、B(5,4)代入y=ax2+bx+c得:
 0= 9a-3b+c
0= 9a-3b+c
4=c ………………………………………2分
4=25a+5b+c
解得:a=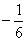 ,b=
,b= ,c=4.
,c=4.
所以y=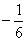 x2+
x2+ x+4……………………………3分
x+4……………………………3分
(2)设AB的解析式为:y=kx+b,……………4分
 把A(-3,0)、B(5,4)代入 0=-3k+b…………………5分
把A(-3,0)、B(5,4)代入 0=-3k+b…………………5分
4=5k+b
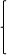 解得: k=
解得: k= .所以AB的解析式为y=
.所以AB的解析式为y= x+
x+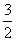 ;……………………6分
;……………………6分
B=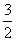 .
.
可设P(x, x+
x+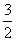 ),Q(x,
),Q(x,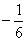 x2+
x2+ x+4),
x+4),
则PQ=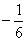 x2+
x2+ x+4-(
x+4-( x+
x+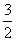 )=
)=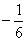 x2+
x2+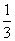 x+
x+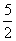 =
=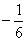 (x-1)2+
(x-1)2+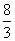 …………7分
…………7分
当x=1时,PQ最大,且最大值为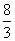 .…………8分
.…………8分
(3)存在.M的坐标为(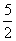 ,9)和(
,9)和(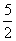 ,-11)…
,-11)…


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
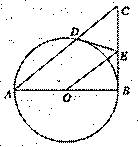
如图,在Rt△ABC中,∠ABC= 90°,以AB为直径的⊙O与AC边交与点D.过D作⊙O的切线交BC与点E.连接OE.
(1)证明:OE∥AC;
(2)①当∠BAC= °时,四边形ODEB是正方形;
②当∠BAC= °时,AD=3DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
某校计划开设4门选修课:音乐、绘画、体育、舞蹈,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门),对调查结果进行统计后,绘制了如下不完整的两个统计图.
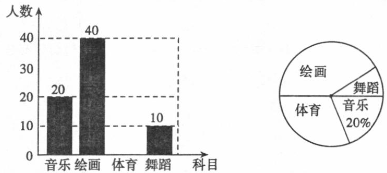
根据以上统计图提供的信息,回答下列问题:
(1)此次调查抽取的学生人数为a=____人,其中选择“绘画”的学生人数占抽样人数的百分比为b=____;
(2)补全条形统计图,并求扇形统计图中“舞蹈”所对应的圆心角的度数;
(3)若该校有2000名学生,请估计全校选择“绘画”的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
观察下列一组坐标:
(a,b),(a,c),(b,c),(b,a),(c,a),(c,b),(a,b),(a,c)…… ,它们是按一定规律排列的,那么第9个坐标是 ,第2015个坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com