
【题目】如图,在平面直角坐标系中,等腰直角三角形OAA1的直角边OA在x轴上,点A1在第一象限,且OA=1,以点A1为直角顶点,0A1为一直角边作等腰直角三角形OA1A2,再以点A2为直角顶点,OA2为直角边作等腰直角三角形OA2A3…依此规律,则点A2019的坐标是_____.
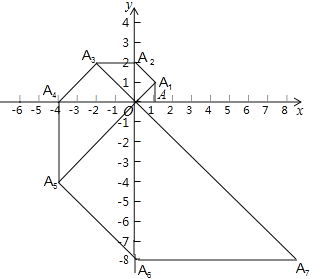
【答案】(﹣21009,21009)
【解析】
利用等腰直角三角形的性质可得出部分点An的坐标,根据点的坐标的变化可得出变化规律“点A8n+3的坐标为(﹣24n+1,24n+1)(n为自然数)”,结合2019=252×8+3即可得出点A2019的坐标.
解:由等腰直角三角形的性质,可知:A1(1,1),A2(0,2),A3(﹣2,2),A4(0,﹣4),A5(﹣4,﹣4),A6(0,﹣8),A7(8,﹣8),A8(16,0),A9(16,16),A10(0,32),A11(﹣32,32),…,
∴点A8n+3的坐标为(﹣24n+1,24n+1)(n为自然数).
∵2019=252×8+3,∴点A2019的坐标为(﹣24×252+1,24×252+1),即(﹣21009,21009),
故答案为(﹣21009,21009).


科目:初中数学 来源: 题型:
【题目】大丰区在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗5棵,B种树苗10棵,需要1300元;购买A种树苗3棵,B种树苗5棵,需要710元.
(1)求购买A,B两种树苗每棵各需要多少元?
(2)现需购进这两种树苗共100棵,其中A种树苗购进x棵,考虑到绿化效果和资金周转,A种树苗不能少于30棵,且用于购买这两种树苗的资金不能超过8650元,试求x 的取值范围。
(3)某包工队承包了该项种植任务,若种好一棵A种树苗需付工钱15元,种好一棵B种树苗需付工钱25元,在(2)的条件下,设种好这100棵树苗共需付工钱y元,,试求出y与x的函数表达式,并写出所付的种植工钱最少的购买方案及最少工钱是多少元。
查看答案和解析>>
科目:初中数学 来源: 题型:
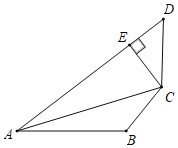
【题目】如图,在四边形ABCD中,CB=CD,∠D+∠ABC=180°,CE⊥AD于E.
(1)求证:AC平分∠DAB;
(2)若AE=3ED=6,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.
(m为常数,m>1,x>0)的图象经过点P(m,1)和Q(1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M分别作x轴和y轴的垂线,垂足分别为A,B.
(1)求∠OCD的度数;
(2)当m=3,1<x<3时,存在点M使得△OPM∽△OCP,求此时点M的坐标;
(3)当m=5时,矩形OAMB与△OPQ的重叠部分的面积能否等于4.1?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
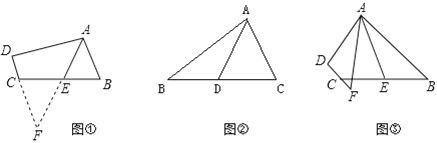
【题目】(1)如图①,在四边形ABCD中,AB∥CD,点E是BC的中点,若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.AB,AD,DC之间的等量关系______.
(2)同题探究.
①如图②,AD是△ABC的中线,AB=6,AC=4,求AD的范围:
②如图③,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,点E是BC的中点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片![]() 放入以
放入以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 边上一点
边上一点![]() 为坐标原点的平面直角坐标系中,连结
为坐标原点的平面直角坐标系中,连结![]() 。将纸片
。将纸片![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 边上点
边上点![]() 处,若
处,若![]() ,则点
,则点![]() 的坐标为________________。
的坐标为________________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=![]() x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
(Ⅰ)求这个二次函数的解析式;
(Ⅱ)连接CP,△DCP是什么特殊形状的三角形?并加以说明;
(Ⅲ)点Q是第一象限的抛物线上一点,且满足∠QEO=∠BEO,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交与点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
(1)求证:∠BCP=∠BAN.
(2)若AC=4,PC=3,求MNBC的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com