
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交与点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.
(1)求证:∠BCP=∠BAN.
(2)若AC=4,PC=3,求MNBC的值.

【答案】(1)证明见解析;(2)![]() ;
;
【解析】
(1)由AC为 O直径,得到∠NAC+∠ACN=90°,由AB=AC,得到∠BAN=∠CAN,根据PC是 O的切线,得到∠ACN+∠PCB=90°,进而可得结论.(2)由等腰三角形的性质得到∠ABC=∠ACB,根据圆内接四边形的性质得到∠PBC=∠AMN,证出△BPC∽△MNA,即可得到结论.
∵AC为⊙O直径,
∴∠ANC=90°,
∴∠NAC+∠ACN=90°,
∵AB=AC,
∴∠BAN=∠CAN,
∵PC是⊙O的切线,
∴∠ACP=90°,
∴∠ACN+∠PCB=90°,
∴∠BCP=∠CAN,
∴∠BCP=∠BAN;
(2)∵AC=4, PC=3,
∴AP=5,
∴PB=1,
∵PC是⊙O的切线,
∴PC2=PMPA,
∴PM=![]() ,
,
∴AM=![]() ,
,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠PBC+∠ABC=∠AMN+∠ACN=180°,
∴∠PBC=∠AMN,
由(1)知∠BCP=∠BAN,
∴△BPC∽△MNA,
∴![]() ,
,
∴MNBC=PBAM=![]() .
.


科目:初中数学 来源: 题型:
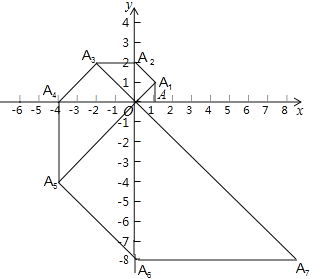
【题目】如图,在平面直角坐标系中,等腰直角三角形OAA1的直角边OA在x轴上,点A1在第一象限,且OA=1,以点A1为直角顶点,0A1为一直角边作等腰直角三角形OA1A2,再以点A2为直角顶点,OA2为直角边作等腰直角三角形OA2A3…依此规律,则点A2019的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按指定的方法解下列方程:
(1)2x2-5x-4=0(配方法);
(2)3(x-2)+x2-2x=0(因式分解法);
(3)(a2-b2)x2-4abx=a2-b2(a2≠b2)(公式法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(4,0),点B(0,6),点P是直线AB上的一个动点,已知点P的坐标为(m,n).
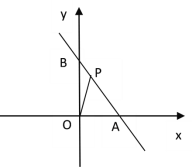
(1)当点P在线段AB上时(不与点A、B重合)
①当m=2,n=3时,求△POA的面积.
②记△POB的面积为S,求S关于m的函数解析式,并写出定义域.
(2)如果S△BOP:S△POA=1:2,请直接写出直线OP的函数解析式.(本小题只要写出结果,不需要写出解题过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,设点
运动,设点![]() 的运动时间为
的运动时间为![]() 秒:
秒:
(1)![]() ________
________![]() ;(用的代数式表示)
;(用的代数式表示)
(2)当![]() 为何值时,
为何值时,![]() ≌
≌![]() ;
;
(3)当点![]() 从点
从点![]() 开始运动,同时,点
开始运动,同时,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,是否存在这样的
运动,是否存在这样的![]() 值,使得
值,使得![]() 与
与![]() 全等?若存在,请求出
全等?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共4只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1 000 |
摸到白球的次数m | 28 | 34 | 48 | 130 | 197 | 251 |
摸到白球的频率 | 0.28 | 0.23 | 0.24 | 0.26 | 0.246 | 0.251 |
(1)请估计:当n很大时,摸到白球的频率将会接近 (精确到0.01);
(2)试估算口袋中白种颜色的球有多少只?
(3)请根据估算的结果思考从口袋中先摸出一球,不放回,再摸出一球,这两只球颜色不同的概率是多少?画出树状图(或列表)表示所有可能的结果,并计算概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com