
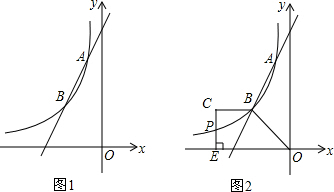
���� ��1����y=$\frac{{k}_{2}}{x}$��ͼ�����A��-1��6�������ô���ϵ����������÷����������Ľ���ʽ���̶���õ�B�����꣬�����ô���ϵ�������һ�κ����Ľ���ʽ��
��2�����ͼ�����k1x+b-$\frac{{k}_{2}}{x}$��0ʱx��ȡֵ��Χ��
��3���������C������Ϊ��m��3����m��0�����÷���S����OBCE=$\frac{1}{2}$��BC+OE��•CE=$\frac{1}{2}$��-2-m-m����3=9���������m��ֵ�����ɵ�P��CE�ϣ�����õ�P�ĺ�����Ϊ-4���̶���ô𰸣�
��� �⣺��1����y=$\frac{{k}_{2}}{x}$��ͼ�����A��-1��6����
��6=$\frac{k}{-1}$��
��k2=-6��
�෴������������ʽΪy=-$\frac{6}{x}$��
�֡�y=-$\frac{6}{x}$����B��a��3����
��a=-2��
���B��-2��3����
��y=k1x+b����A��-1��6������B��-2��3����
��$\left\{\begin{array}{l}{-{k}_{1}+b=6}\\{-2{k}_{1}+b=3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{{k}_{1}=3}\\{b=9}\end{array}\right.$��
��һ�κ�������ʽΪy=3x+9��
��2����ͼ��ã�k1x+b-$\frac{{k}_{2}}{x}$��0ʱx��ȡֵ��ΧΪ��-2��x��-1��x��0��
��3����BC��OE����B��-2��3����
�����C��������m��3����m��0����
��BC=-2-m��
�֡�CE��x���ڵ�E��
���E��������m��0����
��CE=3��OE=-m��
��S����OBCE=$\frac{1}{2}$��BC+OE��•CE=$\frac{1}{2}$��-2-m-m����3=9��
��ã�m=-4��
�ߵ�P��CE�ϣ�
���P�ĺ�����Ϊ-4��
�֡ߵ�P��y=-$\frac{6}{x}$�ϣ�
��y=$\frac{6}{4}$=$\frac{3}{2}$��
���P��������-4��$\frac{3}{2}$����
���� �������ڷ����������ۺ��⣬�����˴���ϵ����������ʽ����Ԫһ�η�����Ľⷨ�Լ����ε����ʣ�ע����������OBCE�����Ϊ9�����췽��S����OBCE=$\frac{1}{2}$��BC+OE��•CE=$\frac{1}{2}$��-2-m-m����3=9�ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{2}$��$\sqrt{2}$=4 | B�� | 2a3•a4=2a12 | C�� | ��2a4��3=8a7 | D�� | a8��a2=a4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com