练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，上、下底面为全等的正六边形礼盒，其主视图与左视图均由矩形构成，主视图中大矩形边长如图所示，左视图中包含两个全等的矩形，如果用彩色胶带按如图所示的方式包扎礼盒，那么所需胶带长度至少为多少厘米？(结果精确到1 cm)

    【答案】432cm

    【解析】分析：由主视图知道，高是20 cm，两顶点之间的最大距离为60 cm，应利用正六边形的性质求得底面对边之间的距离，然后所有棱长相加即可.

    本题解析：

    根据题意，作出实际图形的上底面，如解图．AC，CD是上底面的两边，过点C作CB⊥AD于点B.易得∠ACD＝120°，AC＝CD，CB⊥AD，∴∠CDB＝30°，∴CB＝CD.

    ∵最长对角线长60 cm，∴2CB＋CD＝60 cm，∴CB＝15 cm，CD＝30 cm，∴BD＝15，∴AD＝30 cm.∴胶带的长至少为30×6＋20×6≈432(cm)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

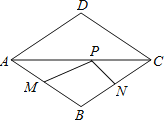
    【题目】如图，点P是边长为1的菱形ABCD对角线AC上的一个动点，点M，N分别是AB，BC边上的中点，则MP+PN的最小值是（　　）

    A. B. 1 C. D. 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用，假定每辆观光车一天内最多只能出租一次，且每辆车的日租金x（元）是5的倍数．发现每天的营运规律如下：当x不超过100元时，观光车能全部租出；当x超过100元时，每辆车的日租金每增加5元，租出去的观光车就会减少1辆．已知所有观光车每天的管理费是1100元．

    （1）优惠活动期间，为使观光车全部租出且每天的净收入为正，则每辆车的日租金至少应为多少元？（注：净收入=租车收入﹣管理费）

    （2）当每辆车的日租金为多少元时，每天的净收入最多？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，AB为⊙O的直径，点C、D在⊙O上，且BC=6cm，AC=8cm，∠ABD=45°．

    （1）求BD的长；

    （2）求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有这样一个问题：探究函数y=-+|x|的图象与性质．
    小军根据学习函数的经验，对函数y=-+|x|的图象与性质进行了探究．
    下面是小军的探究过程，请补充完整：
    （1）函数y=-+|x|的自变量x的取值范围是 ；
    （2）表是y与x的几组对应值.

    x

    -2

    -1.9

    -1.5

    -1

    -0.5

    0

    1

    2

    3

    4

    …

    y

    2

    1.60

    0.80

    0

    -0.72

    -1.41

    -0.37

    0

    0.76

    1.55

    …

    在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；


    （3）观察图象，函数的最小值是 ；
    （4）进一步探究，结合函数的图象，写出该函数的一条性质（函数最小值除外）： ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，三角形DEF是三角形ABC经过某种变换得到的图形，点A与点D，点B与点E，点C与点F分别是对应点，观察点与点的坐标之间的关系，解答下列问题：

    (1)分别写出点A与点D，点B与点E，点C与点F的坐标，并说说对应点的坐标有哪些特征；

    (2)若点P(a＋3，4－b)与点Q(2a，2b－3)也是通过上述变换得到的对应点，求a，b的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．

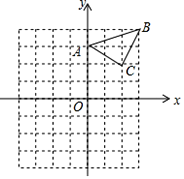
    （1）△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是 ；

    （2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是 ；（画出图形）

    （3）△A2B2C2的面积是 平方单位．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

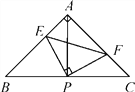
    【题目】如图，已知△ABC中，AB＝AC，∠BAC＝90°，直角∠EPF的顶点P是BC中点，两边PE，PF分别交AB，AC于点E，F，给出以下五个结论：①AE＝CF；②∠APE＝∠CPF；③△EPF是等腰三角形；④EF＝AP；⑤S四边形AEPF＝S△APC.当∠EPF在△ABC内绕顶点P旋转时(点E不与A，B重合)，其中正确的序号有________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边型ABCD中，AB∥DC，过对角线AC的中点O作，分别交边AB,CD于点E,F，连接CE,AF.

    （1）求证：四边形AECF是菱形；

    （2）若EF=8，AE=5，求四边形AECF的面积.

    查看答案和解析>>

    同步练习册答案