Question

11．如图，抛物线y=ax²+bx+c的顶点为C（-1，-2），与x轴交于点A（1，0）和点B．
（1）求抛物线的表达式及直线AC的函数表达式；
（2）点E在抛物线第一象限的图象上，EF∥y轴交直线AC于点F，当EF=AB时，求点E的坐标；
（3）在（2）的条件下，连接BC，点M是线段BC上的一个动点，连接FM，作FN⊥FM交直线BE于点N．
①当点M从点B向点C运动时，$\frac{FN}{FM}$的值是否发生变化？如果变化，请直接写出变化情况；如果不变化，请直接写出这个值；
②当点M在点B的位置时，线段MN的中点为P，当点M在点C的位置时，线段MN的中点为Q，请直接写出线段PQ的长度．

Answer 1

分析 （1）根据抛物线的顶点坐标和点A的坐标确定出抛物线解析式，用待定系数法直接确定出直线AC解析式；
（2）先确定出AB=4，再设出点F的坐标，得出点E坐标，即可得出EF=$\frac{1}{2}$m²-$\frac{1}{2}$，有EF=AB=4，即可求出m，进而得出点E坐标；
（3）①先确定出直线BE解析式，进而得出BE∥AC，再求出FG，CF，最后判断出△FGN∽△FCM得出$\frac{FN}{FM}=\frac{FG}{FC}$=$\frac{1}{2}$，
②利用①方法求出点Q的坐标，再求出点P的坐标，即可得出结论．

解答 解：（1）∵抛物线y=ax²+bx+c的顶点为C（-1，-2），
∴设抛物线解析式为y=a（x+1）²-2，
∵点A（1，0）在抛物线上，
∴a（1+1）²-2=0，
∴a=$\frac{1}{2}$，
∴抛物线解析式为y=$\frac{1}{2}$（x+1）²-2=$\frac{1}{2}$x²+x-$\frac{3}{2}$，
设直线AC解析式为y=kx+b，
∵C（-1，-2），A（1，0）在直线AC上，
∴$\left\{\begin{array}{l}{k+b=0}\\{-k+b=-2}\end{array}\right.$，
∴$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$，
直线AC解析式为y=x-1；
（2）如图1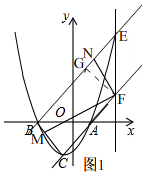，由（1）知，抛物线解析式为y=$\frac{1}{2}$（x+1）²-2，A（1，0），
∴B（-3，0），
∴AB=4，
∵点F在直线AC（y=x-1）上，
设F（m，m-1），
∵EF∥y轴，
∴点E的横坐标为m．
∵点E在抛物线第一象限的图象上，
∴E（m，$\frac{1}{2}$m²+m-$\frac{3}{2}$），
∴EF=$\frac{1}{2}$m²+m-$\frac{3}{2}$-（m-1）=$\frac{1}{2}$m²-$\frac{1}{2}$=4，
∴m=-3（舍）或m=3，
∴E（3，6）；
（3）①当点M从点B向点C运动时，$\frac{FN}{FM}$的值不发生变化，
理由：∵C（-1，-2），B（-3，0），A（1，0），
∴AB=4，BC=2$\sqrt{2}$，AC=2$\sqrt{2}$，
∴BC²+AC²=16=AB²，
∴△ABC是直角三角形，
∴∠ACB=90°，
由（2）知，E（3，6），
∵B（-3，0），
∴直线BE的解析式为y=x+3，
由（1）知，直线AC解析式为y=x-1；
∴BE∥AC，
过点F作FG⊥BE，
∴FG⊥AC，
∵∠CFM+∠GFM=90°，
∵∠FN⊥FM，
∴∠GFN+∠GFM=90°，
∴∠CFM=∠GFN，
∵∠FGN=∠ACB=90°，
∴△FGN∽△FCM，
∴$\frac{FN}{FM}=\frac{FG}{FC}$，
∵∠FGB=∠CFG=∠ACB=90°，
∴四边形BCFG是矩形，
∴FG=BC=2$\sqrt{2}$，
由（2）知，F（3，2），
∵C（-1，-2），
∴FC=$\sqrt{16+16}$=4$\sqrt{2}$，
∴$\frac{FN}{FM}=\frac{FG}{FC}$=$\frac{2\sqrt{2}}{4\sqrt{2}}$=$\frac{1}{2}$；
②如图2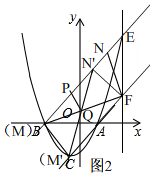，同①的方法得，四边形BCFN'是矩形，
∵当点M在点C的位置时，线段MN的中点为Q，
∴点Q是对角线CN'与BF的交点，
∵B（-3，0），F（3，2），
∴Q（0，1），
同①的方法得，△FN'N∽△FCB，
∴$\frac{NN'}{BC}=\frac{FN}{FM}$=$\frac{1}{2}$，
∴NN'=$\frac{1}{2}$BC=$\sqrt{2}$，
∴BN=BN'+NN'=CF+NN'=5$\sqrt{2}$，
∵点N'在直线BE（y=x+3）的图象上，
设点N'（n，n+3），
∴BN=$\sqrt{2（n+3）^{2}}$=（n+3）$\sqrt{2}$=5$\sqrt{2}$，
∴n=2，∴N（2，5），
∵当点M在点B的位置时，线段MN的中点为P，
∴P（-$\frac{1}{2}$，$\frac{5}{2}$），
∴PQ=$\sqrt{（\frac{1}{2}）^{2}+（\frac{5}{2}-1）^{2}}$=$\frac{\sqrt{10}}{2}$．

点评 此题是二次函数综合题，主要考查了待定系数法，直角三角形的判定和性质，矩形的判定和性质，相似三角形的判定和性质，中点坐标的确定方法，平行线的判定，解本题的关键是判断出BE∥AC和△FGN∽△FCM，是一道很好的中考题．