
| A. | 22+11$\sqrt{3}$ | B. | 22-11$\sqrt{3}$ | C. | 22+11$\sqrt{3}$或22-11$\sqrt{3}$ | D. | 22+11$\sqrt{3}$或2+$\sqrt{3}$ |
分析 分两种情况:①由平行四边形ABCD的面积求出AE=5,AF=6,再根据勾股定理求出BE、DF,求出CE、CF,即可得出结果;
②CE=10-5$\sqrt{3}$,CF=6$\sqrt{3}$-10,即可得出结果.
解答 解:分两种情况:①如图1所示: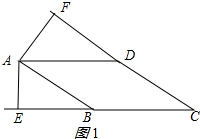 ∠A为锐角时;
∠A为锐角时;
∵平行四边形ABCD的面积=BC•AE=AB•AF=60,AB=10,BC=12,
∴AE=5,AF=6,
∵AE⊥直线BC于点E,作AF⊥直线CD于F,
∴∠AEB=∠AFD=90°,
∴BE=$\sqrt{1{0}^{2}-{5}^{2}}$=5$\sqrt{3}$,DF=$\sqrt{1{2}^{2}-{6}^{2}}$=6$\sqrt{3}$,
∴CE=12+5$\sqrt{3}$,CF=10+6$\sqrt{3}$,
∴CE+CF=22+11$\sqrt{3}$;
②如图2所示: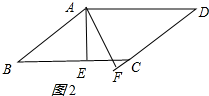 ∠A为钝角时;
∠A为钝角时;
由①得:CE=10-5$\sqrt{3}$,CF=6$\sqrt{3}$-10,
∴CE+CF=2+$\sqrt{3}$;
故选:D.
点评 本题考查了平行四边形的性质、勾股定理以及面积的计算;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键;注意分类讨论,避免漏解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
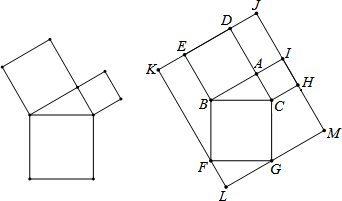
| A. | 48+20$\sqrt{3}$ | B. | 32+20$\sqrt{3}$ | C. | 52+16$\sqrt{3}$ | D. | 28+16$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
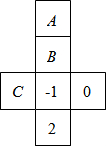 如图,是一个正方形盒子的展开图,若要在展开后的其中的三个正方形A、B、C内分别填入适当的数,使得展开图折成正方体后相对的面上的两个数互为相反数,则填入正方形A、B、C内的三个数依次为( )
如图,是一个正方形盒子的展开图,若要在展开后的其中的三个正方形A、B、C内分别填入适当的数,使得展开图折成正方体后相对的面上的两个数互为相反数,则填入正方形A、B、C内的三个数依次为( )| A. | 1,-2,0 | B. | 0,-2,1 | C. | -2,0,1 | D. | -2,1,0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 职务 | 经理 | 副经理 | 职员 |
| 人数 | 1 | 2 | 12 |
| 月工资(元) | 5000 | 2000 | 800 |
| A. | 2000,2000 | B. | 800,2000 | C. | 2000,800 | D. | 800,800 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -6 | B. | -4 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
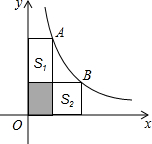 如图,A、B两点在双曲线y=$\frac{4}{x}$上,分别经过A、B两点向x轴,y轴作垂线段,若图中阴影部分的面积为1,则S1+S2=( )
如图,A、B两点在双曲线y=$\frac{4}{x}$上,分别经过A、B两点向x轴,y轴作垂线段,若图中阴影部分的面积为1,则S1+S2=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com