
【题目】如图,一副三角板的两个直角顶点重合在一起.
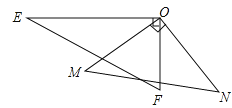
(1)若∠EON=140°,求∠MOF的度数;
(2)比较∠EOM与∠FON的大小,并写出理由;
(3)求∠EON+∠MOF的度数.
【答案】(2)∠MOF=40°,(2)∠EOM=∠FON,(3)180°.
【解析】
试题分析:(1)由∠EOF=90°,∠EON=140°,即可求出∠FON=50°,然后由∠MON=90°,即可求出结果,(2)由余角的性质即可推出∠EOM=∠FON,(3)由图形可知∠EON+∠MOF=∠EOM+∠MOF+∠FON+∠MOF,即可推出∠EON+∠MOF的度数.
试题解析:(1)∵∠EOF=90°,∠EON=140°,
∴∠FON=50°,
∵∠MON=90°,
∴∠MOF=40°,
(2)∠EOM=∠FON,
∵∠EOM+∠MOF=∠FON+∠MOF=90°,
∴∠EOM=∠FON,
(3)∵∠EON+∠MOF=∠EOM+∠MOF+∠FON+∠MOF,
∴∠EON+∠MOF=∠EOF+∠MON=180°.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
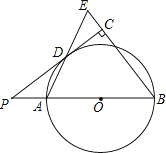
(1)求证:AB=BE;
(2)若PA=2,cosB=![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
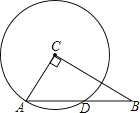
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高饮水质量,越来越多的居民开始选购家用净水器.一商场抓住商机,从厂家购进了A、B两种净水器共160台,A型家用净水器的进价是每台150元,B型净水器的进价是每台350元,购进两种净水器共用去了36000元。
(1)求A、B两种净水器各购进了多少台?
(2)为使每台B型净水器的毛利润是A型净水器的2倍,且保证售完这160台净水器的毛利润不低于11000元,求每台A型净水器的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
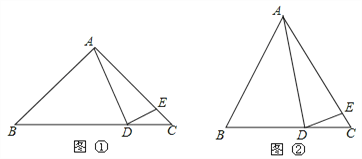
【题目】(14分)探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.
(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;
(3)深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ΔABC和ΔDEF中,已知∠C=∠D,∠B=∠E,要判断这两个三角形全等,还需添加条件( )
A. AB=ED B. AB=FD C. AC=FD D. ∠A =∠F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com