
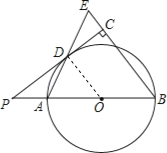
【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
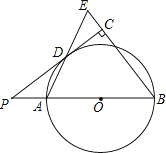
(1)求证:AB=BE;
(2)若PA=2,cosB=![]() ,求⊙O半径的长.
,求⊙O半径的长.
【答案】(1)见解析;(2)3
【解析】
试题分析:(1)本题可连接OD,由PD切⊙O于点D,得到OD⊥PD,由于BE⊥PC,得到OD∥BE,得出∠ADO=∠E,根据等腰三角形的性质和等量代换可得结果;
(2)由(1)知,OD∥BE,得到∠POD=∠B,根据三角函数的定义即可得到结果.
(1)证明:连接OD,
∵PD切⊙O于点D,
∴OD⊥PD,
∵BE⊥PC,
∴OD∥BE,
∴ADO=∠E,
∵OA=OD,
∴∠OAD=∠ADO,
∴∠OAD=∠E,
∴AB=BE;
(2)解:由(1)知,OD∥BE,
∴∠POD=∠B,
∴cos∠POD=cosB=![]() ,
,
在Rt△POD中,cos∠POD=![]() =
=![]() ,
,
∵OD=OA,PO=PA+OA=2+OA,
∴![]() ,
,
∴OA=3,
∴⊙O半径=3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知:如图, AD=CD=CB=AB=a,DA∥CB,AB⊥CB,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.
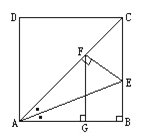
(1)求AC的长;(2)求证:AB=![]() AG.
AG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
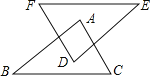
A.AB=DE B.∠B=∠E C.EF=BC D.EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛是我国渤海海峡上的一颗明珠,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向钓鱼岛驶来,渔船向渔政部门报告,并立即返航.渔政船接到报告后,立即从该港口出发赶往钓鱼岛.下图是渔船及渔政船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)

(1)直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.]
(2)求渔船和渔政船相遇时,两船与钓鱼岛的距离.
(3)在渔政船驶往钓鱼岛的过程中,求渔船从港口出发经过多长时间与渔政船相距30海里?
查看答案和解析>>
科目:初中数学 来源: 题型:
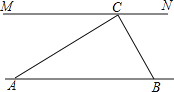
【题目】为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留整数)
≈1.73,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
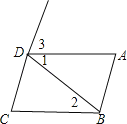
【题目】推理填空:如图:
①若∠1=∠2,
则 ∥ (内错角相等,两直线平行);
若∠DAB+∠ABC=180°,
则 ∥ (同旁内角互补,两直线平行);
②当 ∥ 时,
∠C+∠ABC=180°(两直线平行,同旁内角互补);
③当 ∥ 时,
∠3=∠C (两直线平行,同位角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一副三角板的两个直角顶点重合在一起.
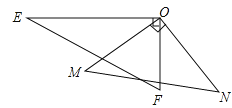
(1)若∠EON=140°,求∠MOF的度数;
(2)比较∠EOM与∠FON的大小,并写出理由;
(3)求∠EON+∠MOF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com