练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一个质地均匀的小正方体，六个面上分别标有数字1，1，2，4，5，6，掷一次小正方体，观察朝上一面的数字．

    (1)朝上的数字是“3”的事件是什么事件？它的概率是多少？

    (2)朝上的数字是“1”的事件是什么事件？它的概率是多少？

    (3)朝上的数字是偶数的事件是什么事件？它的概率是多少？

    【答案】（1）不可能事件，0（2）随机事件，（3）随机事件，

    【解析】

    （1）由于数字中没有数字“3”，因此朝上的数字是“3”的事件是不可能事件，由此即可求得概率；

    （2）朝上一面的数字一共有6种等可能的情况，其中出现数字“1”是随机事件，然后根据概率公式进行计算即可；

    （3）朝上一面的数字可能是奇数也可能是偶数，可知事件为随机事件，然后根据概率公式进行计算即可.

    抛掷这个小正方体，朝上一面的数字有“1”、“1”、“2”、“4”、“5”、“6”共6种等可能的情况，

    (1)数字中没有3，因此朝上的数字是“3”的事件是不可能事件，

    它的概率为0；

    (2)朝上的数字为“1”占有两种情况，所以朝上的数字是“1”的事件是随机事件，

    它的概率为；

    (3)朝上的数字为偶数有三种情况，所以朝上的数字是偶数的事件是随机事件，

    它的概率为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】.在一次课题设计活动中，小明对修建一座87m长的水库大坝提出了以下方案；大坝的横截面为等腰梯形，如图，∥，坝高10m，迎水坡面的坡度，老师看后，从力学的角度对此方案提出了建议，小明决定在原方案的基础上，将迎水坡面的坡度进行修改，修改后的迎水坡面的坡度。

    1. 求原方案中此大坝迎水坡的长（结果保留根号）
    2. 如果方案修改前后，修建大坝所需土石方总体积不变，在方案修改后，若坝顶沿方向拓宽2.7m，求坝顶将会沿方向加宽多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利45元，为了扩大销售、增加盈利尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出4件，若商场平均每天盈利2100元，每件衬衫应降价多少元？请完成下列问题：

    （1）未降价之前，某商场衬衫的总盈利为　 　 元．

    （2）降价后，设某商场每件衬衫应降价x元，则每件衬衫盈利　 　元，平均每天可售出　 　件（用含x的代数式进行表示）

    （3）请列出方程，求出x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】今年本市蜜桔大丰收，某水果商销售一种蜜桔，成本价为10元/千克，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于18元/千克，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）之间的函数关系如图所示：

    （1）求y与x之间的函数关系式；

    （2）该经销商想要每天获得150元的销售利润，销售价应定为多少？

    （销售利润=销售价－成本价）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点M、N是∠ABC与∠ACB三等分线的交点，若∠A=60°，则∠BMN的度数是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数（，、、为常数）的图象如图所示，下列个结论：①；②；③；④；⑤为常数，且．其中正确的结论有（ ）

    A. 2个 B. 3个 C. 4个 D. 5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】x2+(p+q)x+pq型式子是数学学习中常见的一类多项式，如何将这种类型的式子因式分解呢？因为(x+p)(x+q)= x2+(p+q)x+pq，所以，根据因式分解是与整式乘法方向相反的变形，利用这种关系可得：x2+(p+q)x+pq=(x+p)(x+q).如：x2+3x+2=x2+(1+2)x+1×2=(x+1)(x+2)，上述过程还可以形象的用十字相乘的形式表示:先分解二次项系数，分别写在十字交叉线的左上角和左下角；再分解常数项，分别写在十字交叉线的右上角和右下角；然后交叉相乘，求代数和，使其等于一次项的系数，如下图.这样，我们可以得到：x2+3x+2= (x+1)(x+2)，利用这种方法，将下列多项式分解因式：

    （1）x2+7x+10

    （2）－2x2－6x+36

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】两块等腰直角三角板△ABC和△DEC如图摆放，其中∠ACB=∠DCE=90°，F是DE的中点，H是AE的中点，G是BD的中点．

    （1）如图1，若点D、E分别在AC、BC的延长线上，通过观察和测量，猜想FH和FG的数量关系为______和位置关系为______；

    （2）如图2，若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时，其余条件均不变，则（1）中的猜想是否还成立，若成立，请证明，不成立请说明理由；

    （3）如图3，将图1中的△DEC绕点C顺时针旋转一个锐角，得到图3，（1）中的猜想还成立吗？写出结论，证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB＜BC，E为CD边的中点，将△ADE绕点E顺时针旋转180°，点D的对应点为C，点A的对应点为F，过点E作ME⊥AF交BC于点M，连接AM、BD交于点N，现有下列结论：

    ①AM=AD+MC；②AM=DE+BM；③DE2=ADCM；④点N为△ABM的外心．其中正确的个数为（　　）

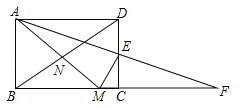
    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    同步练习册答案