
����Ŀ���������ֱ�����ǰ���ABC����DEC��ͼ�ڷţ�������ACB=��DCE=90����F��DE���е㣬H��AE���е㣬G��BD���е㣮

��1����ͼ1������D��E�ֱ���AC��BC���ӳ����ϣ�ͨ���۲�Ͳ���������FH��FG��������ϵΪ______��λ�ù�ϵΪ______��
��2����ͼ2���������ǰ���DEC���ŵ�C˳ʱ����ת��ACE��һ��ֱ����ʱ���������������䣬��1���еIJ����Ƿ���������������֤������������˵�����ɣ�
��3����ͼ3����ͼ1�е���DEC�Ƶ�C˳ʱ����תһ����ǣ��õ�ͼ3����1���еIJ��뻹������д�����ۣ�֤����
���𰸡���1����ȣ���ֱ����2��������֤������������3��������������FH=FG��FH��FG��֤��������.
��������
��1��֤AD=BE�����������ε���λ���Ƴ�FH=![]() AD��FH��AD��FG=
AD��FH��AD��FG=![]() BE��FG��BE�������Ƴ��𰸣�
BE��FG��BE�������Ƴ��𰸣�
��2��֤��ACD�ա�BCE���Ƴ�AD=BE�����������ε���λ�߶��������Ƴ��𰸣�
��3������BE��AD������ȫ���Ƴ�AD=BE�����������ε���λ�߶��������Ƴ��𰸣�
��1����CE=CD��AC=BC����ECA=��DCB=90����
��BE=AD��
��F��DE���е㣬H��AE���е㣬G��BD���е㣬
��FH=![]() AD��FH��AD��FG=
AD��FH��AD��FG=![]() BE��FG��BE��
BE��FG��BE��
��FH=FG��
��AD��BE��
��FH��FG��
�ʴ�Ϊ����ȣ���ֱ��
��2���𣺳�����
֤������CE=CD����ECD=��ACD=90����AC=BC��
���ACD�ա�BCE
��AD=BE��
�ɣ�1��֪��FH=![]() AD��FH��AD��FG=
AD��FH��AD��FG=![]() BE��FG��BE��
BE��FG��BE��
��FH=FG��FH��FG��
�ࣨ1���еIJ��뻹������

��3���𣺳�����������FH=FG��FH��FG��
����AD��BE�����߽���Z��AD��BC��X��
ͬ��1����֤
��FH=![]() AD��FH��AD��FG=
AD��FH��AD��FG=![]() BE��FG��BE��
BE��FG��BE��
��������ECD��ACB�ǵ���ֱ�������Σ�
��CE=CD��AC=BC����ECD=��ACB=90����
���ACD=��BCE��
����ACD����BCE��
 ��
��
���ACD�ա�BCE��
��AD=BE����EBC=��DAC��
�ߡ�DAC+��CXA=90������CXA=��DXB��
���DXB+��EBC=90����
���EZA=180����90��=90����
��AD��BE��
��FH��AD��FG��BE��
��FH��FG��
��FH=FG��FH��FG��
������FH=FG��FH��FG.


 ��ʦ����ָ���ο�ʱϵ�д�
��ʦ����ָ���ο�ʱϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
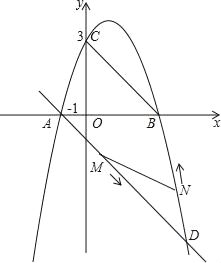
����Ŀ����ͼ�����κ���y=ax2+2x+c��ͼ����x�ύ�ڵ�A����1��0���͵�B����y�ύ�ڵ�C��0��3����
��1����ö��κ����ı���ʽ��
��2������A��ֱ��AD��BC�ҽ�����������һ��D����ֱ��AD�ĺ�������ʽ��
��3���ڣ�2���������£������������⣺
����x�����Ƿ����һ��P��ʹ����B��C��PΪ���������������ABD���ƣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
������M��ÿ��1����λ���ٶ����߶�AD�ӵ�A���D�˶���ͬʱ������N��ÿ��![]() ����λ���ٶ����߶�DB�ӵ�D���B�˶����ʣ����˶������У����˶�ʱ��tΪ��ֵʱ����DMN�����������������ֵ��
����λ���ٶ����߶�DB�ӵ�D���B�˶����ʣ����˶������У����˶�ʱ��tΪ��ֵʱ����DMN�����������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ʵؾ��ȵ�С�����壬�������Ϸֱ��������1��1��2��4��5��6����һ��С�����壬�۲쳯��һ������֣�
(1)���ϵ������ǡ�3�����¼���ʲô�¼������ĸ����Ƕ��٣�
(2)���ϵ������ǡ�1�����¼���ʲô�¼������ĸ����Ƕ��٣�
(3)���ϵ�������ż�����¼���ʲô�¼������ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
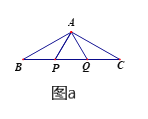
����Ŀ����ͼa��P��Q�ǡ�ABC�ı�BC�ϵ����㣬�ҡ�APQΪ�ȱ������Σ�AB=AC,
��1����֤��BP=CQ.
��2����ͼa������BAC=120![]() ��AP=3����BC�ij�.
��AP=3����BC�ij�.
��3������BAC=120![]() ����ֱ��BC����ƽ���ƶ���APQ�õ���A��P��Q������ͼb����A��Q����AC���ڵ�M.����P�ƶ����δ�ʱ����AA��M�ա�CQ��M��֤����Ľ���.
����ֱ��BC����ƽ���ƶ���APQ�õ���A��P��Q������ͼb����A��Q����AC���ڵ�M.����P�ƶ����δ�ʱ����AA��M�ա�CQ��M��֤����Ľ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y��kx+k��2�����㣨m��n+1���ͣ�m+1��2n+3�����ҩ�2��k��0����n��ȡֵ��Χ�ǣ�������
A. ��2��n��0B. ��4��n����2C. ��4��n��0D. 0��n����2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵�ƻ�����A��B�����ͺŵĵ綯���г���30��������A�͵綯���г�������20����A��B�����ͺŵ綯���г��Ľ������۷ֱ�Ϊ2500Ԫ��3000Ԫ���ۼ۷ֱ�Ϊ2800Ԫ��3500Ԫ������̵�ƻ�����A�͵綯���г�m���������ͺŵĵ綯���г�ȫ�����ۺ�ɻ�����yԪ��
��1�����y��m֮��ĺ�����ϵʽ��
��2�����̵���ν������ܻ���������ʱ��������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD��AF�ֱ�Ϊ��ABC�����ߺߣ�BEΪ��ABD�Ľ�ƽ���ߣ�

��1������BED=40������BAD=25�������BAF�Ĵ�С��
��2������ABC�����Ϊ40��BD=5����AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��趨��һ����������ת����ת�̣�ת�̱��ȷֳ�16�����Σ������涨���˿����̳�����ÿ��200Ԫ�����ܻ��һ��ת��ת�̵Ļ��ᣮ���ת��ֹͣ��ָ�����ö��졢�ƺ���ɫ���˿;Ϳ��Էֱ���50Ԫ��30Ԫ��10Ԫ�Ĺ���ȯ������˿Ͳ�Ը��תת�̣������ֱ�ӻ�ù���ȯ15Ԫ��
(1)ת��һ��ת�̣����50Ԫ��30Ԫ��10Ԫ����ȯ�ĸ��ʷֱ��Ƕ��٣�
(2)�����һ���˿����̳�������200Ԫ��ͨ������˵��תת�̺�ֱ�ӻ�ù���ȯ�����ַ�ʽ����λ�˿����㣿

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
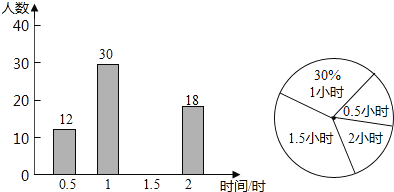
����Ŀ��Ϊ�����ѧ���Ķ�����������ijУ������꼶ѧ������˫���ռ�ǿ�����Ķ���Ϊ�˽�ͬѧ���Ķ��������ѧУ�������˲���ͬѧ��ĩ�Ķ�ʱ�䣬���ҵõ����ݻ����˲�������ͳ��ͼ������ͼ����Ϣ�ش��������⣺
��1��������ͳ��ͼ�����������������ѧ����ĩ�Ķ�ʱ�������Ƕ���Сʱ����λ���Ƕ���Сʱ��
��2�����㱻����ѧ���Ķ�ʱ���ƽ������
��3����У���꼶����500�ˣ��Թ�����ĩ�Ķ�ʱ�䲻����1.5Сʱ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com