
����Ŀ��ij�̵�ƻ�����A��B�����ͺŵĵ綯���г���30��������A�͵綯���г�������20����A��B�����ͺŵ綯���г��Ľ������۷ֱ�Ϊ2500Ԫ��3000Ԫ���ۼ۷ֱ�Ϊ2800Ԫ��3500Ԫ������̵�ƻ�����A�͵綯���г�m���������ͺŵĵ綯���г�ȫ�����ۺ�ɻ�����yԪ��
��1�����y��m֮��ĺ�����ϵʽ��
��2�����̵���ν������ܻ���������ʱ��������Ƕ���Ԫ��
���𰸡���1��![]() ����200
����200![]() +15000��20��m��30������2�� ����A�͵綯���г�20��������B��10�������������11000Ԫ��
+15000��20��m��30������2�� ����A�͵綯���г�20��������B��10�������������11000Ԫ��
��������
��1������=һ��A�͵綯���г���������A�͵綯���г�������+һ��B�͵綯���г���������B�͵綯���г���������������ʽ���ɣ�
��2������һ�κ��������ʣ�����Ա�����ȡֵ��Χ������⣻
�⣺��1���ƻ�����A�͵綯���г�![]() ����B�͵綯���г���30-
����B�͵綯���г���30-![]() ������
������
![]() ����2800-2500��m+��3500��3000����30��m����
����2800-2500��m+��3500��3000����30��m����
����200![]() +15000��20��m��30����
+15000��20��m��30����
��2����20��![]() ��30����
��30����![]() ��
��![]() ���������С�ɵã�
���������С�ɵã�![]() ��20ʱ��
��20ʱ��![]() �����ֵ��
�����ֵ��
![]() ����200��20+15000��11000��
����200��20+15000��11000��
����A�͵綯���г�20��������B��10�������������11000Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�յ�Ǯ�����۳���Ϣ��ͼ��

��������Ϣ��С�콫�����泱���γɺ�ͷ���ҵ�֮��ľ���s��ǧ�ף���ʱ��t�����ӣ��ĺ�����ϵ��ͼ3��ʾ�����У���11��40ʱ�������泱���ij�ͷ���ҵ�12ǧ������Ϊ��A��0��12������B����Ϊ��m��0��������BC���ö��κ���s=![]() t2+bt+c��b��c�dz������̻���
t2+bt+c��b��c�dz������̻���
��1����m��ֵ���������ͷ�Ӽص��ҵص��ٶȣ�
��2��11��59ʱ��С���ﵥ�����ҵس������ؽ��߹�·��0.48ǧ��/�ֵ��ٶ����ط���ȥ���������������Ӻ��볱ͷ������
��3��������С��������ת��ͷ���ؽ��߹�·����ͷ�ٶ��볱ͷ���У�����ͷ���ҵغ���ȼ��٣�����������ٶ�Ϊ0.48ǧ��/�֣�С���������С���볱ͷ���������ͷ1.8ǧ����ʱ�䣿����ˮ���ٽ��ٶ�v=v0+![]() ��t��30����v0�Ǽ���ǰ���ٶȣ���
��t��30����v0�Ǽ���ǰ���ٶȣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧѧϰ��վΪ����������ע����룬������һ��Ϊ��5����ƹ�.�ڻ�ڼ䣬�������վ�������仯������±���ʾ:
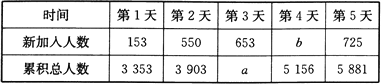
(1)������![]() ��
�� ![]() ��
��
(2)������������ͳ��ͼ��������;
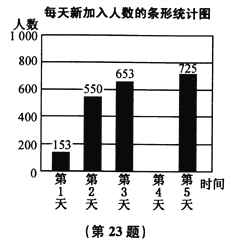
(3)����������Ϣ������˵����ȷ���� (ֻҪ��д��ȷ˵��ǰ�����).
���ڻ֮ǰ������վ����3 200�˼���;
���ڻ�ڼ䣬ÿ���¼��������������;
���ڻ�ڼ䣬����վ�¼����������Ϊ2 528��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������к������ú���a��b�Ĵ���ʽ��ʾ��Ӧͼ�ε������
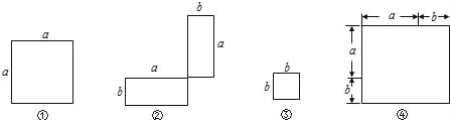
�� �� �� ��
��ͨ��ƴͼ���㷢��ǰ����ͼ�ε��������ĸ�ͼ�����֮����ʲô��ϵ�� ������ѧʽ�ӱ�ʾ�� ��
�����ã�2���Ľ��ۼ��㣺
��![]()
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=kx+b������A��-5��0����B��-1��4��
��1����ֱ��AB�ı���ʽ��
��2����ֱ��CE��y=-2x-4��ֱ��AB��y��Χ��ͼ�ε������
��3������ͼ��ֱ��д������x�IJ���ʽkx+b��-2x-4�Ľ⼯��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��B�����������ϣ���A��ԭ��O����ߣ���ʾ����Ϊ��10����B��ԭ����ұߣ���BO��3AO����M��ÿ��3����λ���ȵ��ٶȴӵ�A���������˶�����N��ÿ��2����λ���ȵ��ٶȴӵ�O���������˶�����M����Nͬʱ��������
��1�������ϵ�B��Ӧ�������� ������B����A�ľ������� ����
��2���������룬ԭ��O���߶�MN���е㣿
��3���������룬��M��N�ֱ�B�ľ�����ȣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
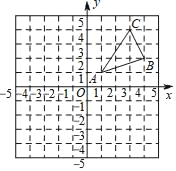
����Ŀ����ͼ����ABC�������������ֱ�ΪA��1��1����B��4��2����C��3��4����
��1���뻭����ABC����ԭ��ԳƵ���A1B1C1����д����A1��B1��C1�����꣮
��2���뻭����ABC��O˳ʱ����ת90�������A2B2C2����д����A2��B2��C2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
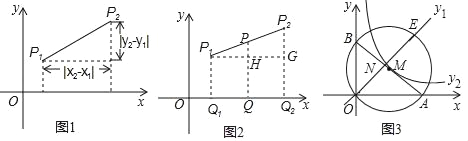
����Ŀ���Ķ����⣺����������ѧ��������Ҫ�о��������Ǿ����������ν�ϣ�����ת���ķ������һЩ��ѧ���⣬С������ͬһ�������������ľ���ʱ���֣�����ƽ��ֱ������ϵ����������P1��x1��y1����P2��x2��y2������ͨ������ֱ������������ͼ1�õ����ۣ�P1P2=![]() ����������ͼ2֤�����߶�P1P2���е�P��x��y����P�����깫ʽ��x=
����������ͼ2֤�����߶�P1P2���е�P��x��y����P�����깫ʽ��x=![]() ��y=
��y=![]() ��
��
����Ӧ�ã�
��ͼ3����ƽ��ֱ������ϵ�У���֪A��8��0����B��0��6����C��1��7������M����ԭ��O����A��B��
��1�����M�İ뾶��Բ��M�����ꣻ
��2���жϵ�C���M��λ�ù�ϵ����˵�����ɣ�
��3������BOA��ƽ���߽�AB�ڵ�N������M�ڵ�E���ֱ����OE�ı���ʽy1������M�ķ����������ı���ʽy2��������ͼ��y2��y1��0ʱ����ֱ��д��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������쳵���й���20������֪ÿ������ÿ�������������6�����������5������ÿ����һ������������ɻ�����150Ԫ��ÿ����һ����������ɻ�����260Ԫ������20�������У�����ÿ�찲��![]() ��������������������������������������������������ĸ����������������������һ�룮
��������������������������������������������������ĸ����������������������һ�룮
��1����д���˳���ÿ����������![]() ��Ԫ����
��Ԫ����![]() ���ˣ�֮��ĺ�����ϵʽ��
���ˣ�֮��ĺ�����ϵʽ��
��2�����Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��������������ÿ���õ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com