
ЁОЬтФПЁПШчЭМЃЌФГШеЕФЧЎЬСНЙлГБаХЯЂШчЭМЃК

АДЩЯЪіаХЯЂЃЌаЁКьНЋЁАНЛВцГБЁБаЮГЩКѓГБЭЗгыввЕижЎМфЕФОрРыsЃЈЧЇУзЃЉгыЪБМфtЃЈЗжжгЃЉЕФКЏЪ§ЙиЯЕгУЭМ3БэЪОЃЌЦфжаЃКЁА11ЃК40ЪБМзЕиЁЎНЛВцГБЁЏЕФГБЭЗРыввЕи12ЧЇУзЁБМЧЮЊЕуAЃЈ0ЃЌ12ЃЉЃЌЕуBзјБъЮЊЃЈmЃЌ0ЃЉЃЌЧњЯпBCПЩгУЖўДЮКЏЪ§s=![]() t2+bt+cЃЈbЃЌcЪЧГЃЪ§ЃЉПЬЛЃЎ
t2+bt+cЃЈbЃЌcЪЧГЃЪ§ЃЉПЬЛЃЎ
ЃЈ1ЃЉЧѓmЕФжЕЃЌВЂЧѓГіГБЭЗДгМзЕиЕНввЕиЕФЫйЖШЃЛ
ЃЈ2ЃЉ11ЃК59ЪБЃЌаЁКьЦяЕЅГЕДгввЕиГіЗЂЃЌбиНБпЙЋТЗвд0.48ЧЇУз/ЗжЕФЫйЖШЭљМзЕиЗНЯђШЅПДГБЃЌЮЪЫ§МИЗжжгКѓгыГБЭЗЯргіЃП
ЃЈ3ЃЉЯргіКѓЃЌаЁКьСЂМДЕїзЊГЕЭЗЃЌбиНБпЙЋТЗАДГБЭЗЫйЖШгыГБЭЗВЂааЃЌЕЋГБЭЗЙ§ввЕиКѓОљдШМгЫйЃЌЖјЕЅГЕзюИпЫйЖШЮЊ0.48ЧЇУз/ЗжЃЌаЁКьж№НЅТфКѓЃЎЮЪаЁКьгыГБЭЗЯргіЕНТфКѓГБЭЗ1.8ЧЇУзЙВашЖрГЄЪБМфЃПЃЈГБЫЎМгЫйНзЖЮЫйЖШv=v0+![]() ЃЈtЉ30ЃЉЃЌv0ЪЧМгЫйЧАЕФЫйЖШЃЉЃЎ
ЃЈtЉ30ЃЉЃЌv0ЪЧМгЫйЧАЕФЫйЖШЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉ0.4ЧЇУз/ЗжжгЃЌЃЈ2ЃЉ5ЗжжгЃЛЃЈ3ЃЉ26ЗжжгЃЌ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЬтвтПЩжЊЃКОЙ§30ЗжжгКѓЕНДяввЕиЃЌДгЖјПЩжЊm=30ЃЌгЩгкМзЕиЕНввЕиЪЧдШЫйдЫЖЏЃЌЫљвдРћгУТЗГЬГ§вдЪБМфМДПЩЧѓГіЫйЖШЃЛ
ЃЈ2ЃЉгЩгкГБЭЗЕФЫйЖШЮЊ0.4ЧЇУз/ЗжжгЃЌЫљвдЕН11ЃК59ЪБЃЌГБЭЗвбЧАНј19ЁС0.4=7.6ЧЇУзЃЌЩшаЁКьГіЗЂxЗжжгЃЌИљОнЬтвтСаГіЗНГЬМДПЩЧѓГіxЕФжЕЃЌ
ЃЈ3ЃЉЯШЧѓГіsЕФНтЮіЪНЃЌИљОнГБЫЎМгЫйНзЖЮЕФЙиЯЕЪНЃЌЧѓГіГБЭЗЕФЫйЖШДяЕНЕЅГЕзюИпЫйЖШ0.48ЧЇУз/ЗжжгЪБЫљЖдгІЕФЪБМфtЃЌДгЖјПЩжЊГБЭЗгыввЕижЎМфЕФОрРыsЃЌЩшЫ§РыввЕиЕФОрРыЮЊs1ЃЌдђs1гыЪБМфtЕФКЏЪ§ЙиЯЕЪНЮЊs1=0.48t+hЃЈtЁн35ЃЉЃЌЕБt=35ЪБЃЌs1=s=![]() ЃЌДгЖјПЩЧѓГіhЕФжЕЃЌзюКѓГБЭЗгыаЁКьЯрОр1.8ЧЇУзЪБЃЌМДs-s1=1.8ЃЌДгЖјПЩЧѓГіtЕФжЕЃЌгЩгкаЁКьгыГБЭЗЯргіКѓЃЌАДГБЭЗЫйЖШгыГБЭЗВЂааЕНДяввЕигУЪБ6ЗжжгЃЌЙВашвЊЪБМфЮЊ6+50-30=26ЗжжгЃЌ
ЃЌДгЖјПЩЧѓГіhЕФжЕЃЌзюКѓГБЭЗгыаЁКьЯрОр1.8ЧЇУзЪБЃЌМДs-s1=1.8ЃЌДгЖјПЩЧѓГіtЕФжЕЃЌгЩгкаЁКьгыГБЭЗЯргіКѓЃЌАДГБЭЗЫйЖШгыГБЭЗВЂааЕНДяввЕигУЪБ6ЗжжгЃЌЙВашвЊЪБМфЮЊ6+50-30=26ЗжжгЃЌ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉгЩЬтвтПЩжЊЃКm=30ЃЌЁрBЃЈ30ЃЌ0ЃЉЃЌГБЭЗДгМзЕиЕНввЕиЕФЫйЖШЮЊЃК![]() ЃН0.4ЧЇУз/ЗжжгЃЛ
ЃН0.4ЧЇУз/ЗжжгЃЛ
ЃЈ2ЃЉЁпГБЭЗЕФЫйЖШЮЊ0.4ЧЇУз/ЗжжгЃЌЁрЕН11ЃК59ЪБЃЌГБЭЗвбЧАНј19ЁС0.4=7.6ЧЇУзЃЎ
ЩшаЁКьГіЗЂxЗжжггыГБЭЗЯргіЃЌЁр0.4x+0.48x=12-7.6ЃЌЁрx=5ЃЌЁраЁКь5ЗжжггыГБЭЗЯргіЃЎ
ЃЈ3ЃЉАбЃЈ30ЃЌ0ЃЉЃЌCЃЈ55ЃЌ15ЃЉДњШыs=![]() t2+bt+cЃЌНтЕУЃКb=-
t2+bt+cЃЌНтЕУЃКb=-![]() ЃЌc=-
ЃЌc=-![]() ЃЌЁрs=
ЃЌЁрs=![]() t2-
t2-![]() t-
t-![]() ЃЎ
ЃЎ
Ёпv0=0.4ЃЌЁрv=![]() ЃЈt-30ЃЉ+
ЃЈt-30ЃЉ+![]() ЃЎ
ЃЎ
ЕБГБЭЗЕФЫйЖШДяЕНЕЅГЕзюИпЫйЖШ0.48ЧЇУз/ЗжжгЃЌДЫЪБv=0.48ЃЌЁр0.48=![]() ЃЈt-30ЃЉ+
ЃЈt-30ЃЉ+![]() ЃЌЁрt=35ЃЎ
ЃЌЁрt=35ЃЎ
ЕБt=35ЪБЃЌs=![]() t2-
t2-![]() t-
t-![]() =
=![]() ЃЌЁрДгt=35ЗжЃЈ12ЃК15ЪБЃЉПЊЪМЃЌГБЭЗПьгкаЁКьЫйЖШБМЯђБћЕиЃЌаЁКьж№НЅТфКѓЃЌЕБаЁКьШдвд0.48ЧЇУз/ЗжЕФЫйЖШдШЫйзЗИЯГБЭЗЃЎ
ЃЌЁрДгt=35ЗжЃЈ12ЃК15ЪБЃЉПЊЪМЃЌГБЭЗПьгкаЁКьЫйЖШБМЯђБћЕиЃЌаЁКьж№НЅТфКѓЃЌЕБаЁКьШдвд0.48ЧЇУз/ЗжЕФЫйЖШдШЫйзЗИЯГБЭЗЃЎ
ЩшЫ§РыввЕиЕФОрРыЮЊs1ЃЌдђs1гыЪБМфtЕФКЏЪ§ЙиЯЕЪНЮЊs1=0.48t+hЃЈtЁн35ЃЉЃЎ
ЕБt=35ЪБЃЌs1=s=![]() ЃЌДњШыПЩЕУЃКh=-
ЃЌДњШыПЩЕУЃКh=-![]() ЃЌЁрs1=
ЃЌЁрs1=![]() t-
t-![]() ЃЎ
ЃЎ
зюКѓГБЭЗгыаЁКьЯрОр1.8ЧЇУзЪБЃЌМДs-s1=1.8ЃЌЁр![]() t2-
t2-![]() t-
t-![]() -
-![]() t+
t+![]() =1.8
=1.8
НтЕУЃКt=50Лђt=20ЃЈВЛЗћКЯЬтвтЃЌЩсШЅЃЉЃЌЁрt=50ЃЎ
аЁКьгыГБЭЗЯргіКѓЃЌАДГБЭЗЫйЖШгыГБЭЗВЂааЕНДяввЕигУЪБ6ЗжжгЃЌЁрЙВашвЊЪБМфЮЊ6+50-30=26ЗжжгЃЎ
ЙЪаЁКьгыГБЭЗЯргіЕНГБЭЗРыЫ§1.8ЧЇУзЭтЙВашвЊ26ЗжжгЃЎ


 жБЭЈЙѓжнУћаЃжмВтдТПМжБЭЈУћаЃЯЕСаД№АИ
жБЭЈЙѓжнУћаЃжмВтдТПМжБЭЈУћаЃЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌAOЪЧЁїABCЕФНЧЦНЗжЯпЃЎвдOЮЊдВаФЃЌOCЮЊАыОЖзїЁбOЃЎ
ЃЈ1ЃЉЧѓжЄЃКABЪЧЁбOЕФЧаЯпЃЎ
ЃЈ2ЃЉвбжЊAOНЛЁбOгкЕуEЃЌбгГЄAOНЛЁбOгкЕуDЃЌtanD=![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ3ЃЉЃЈ3ЗжЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЩшЁбOЕФАыОЖЮЊ3ЃЌЧѓABЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉдкЯТСаКсЯпЩЯгУКЌгаaЃЌbЕФДњЪ§ЪНБэЪОЯргІЭМаЮЕФУцЛ§ЃЎ
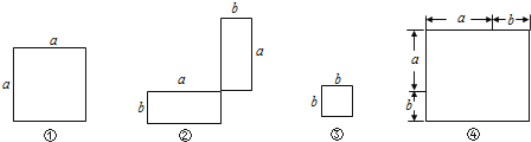
ЂйЁЁ ЁЁЃЛ ЂкЁЁ ЁЁЃЛ ЂлЁЁ ЁЁЃЛ ЂмЁЁ ЁЁЃЎ
ЃЈ2ЃЉЭЈЙ§ЦДЭМЃЌФуЗЂЯжЧАШ§ИіЭМаЮЕФУцЛ§гыЕкЫФИіЭМаЮУцЛ§жЎМфгаЪВУДЙиЯЕЃПЧыгУЪ§бЇЪНзгБэЪОЃКЁЁ ЁЁЃЛ
ЃЈ3ЃЉРћгУЃЈ2ЃЉЕФНсТлМЦЫу992+2ЁС99ЁС1+1ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯB=30ЁуЃЌADЦНЗжЁЯBAC,DEЁЭABгкE,гаЯТСаНсТлЃКЂйDE=DCЃЛЂкЁЯBDE=ЁЯADCЃЛЂлAB=2ACЃЛЂмЭМжаЙВгаСНЖдШЋЕШШ§НЧаЮ.Цфжае§ШЗЕФЪЧЃК____________ЃЈЬюађКХМДПЩЃЉ.
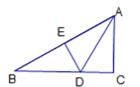
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌABЃН4ЃЌЕуEЪЧЖдНЧЯпACЩЯЕФвЛЕуЃЌСЌНгDEЃЎЙ§ЕуEзїEFЁЭEDЃЌНЛABгкЕуFЃЌвдDEЁЂEFЮЊСкБпзїОиаЮDEFGЃЌСЌНгAGЃЎ
ЃЈ1ЃЉЧѓжЄЃКОиаЮDEFGЪЧе§ЗНаЮЃЛ
ЃЈ2ЃЉЧѓAG+AEЕФжЕЃЛ
ЃЈ3ЃЉШєFЧЁЮЊABжаЕуЃЌСЌНгDFНЛACгкЕуMЃЌЧыжБНгаДГіMEЕФГЄЃЎ
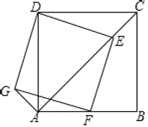
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊСтаЮЕФБпГЄКЭвЛЬѕЖдНЧЯпЕФГЄОљЮЊ2 cmЃЌдђСтаЮЕФУцЛ§ЮЊ( )
A. 3cm2 B. 4 cm2 C. ![]() cm2 D. 2
cm2 D. 2![]() cm2
cm2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃОіЖЈЖдбЇЩњИааЫШЄЕФЧђРрЯюФП(A:зуЧђЃЌB:РКЧђЃЌC:ХХЧђЃЌD:г№УЋЧђЃЌE:ЦЙХвЧђ)НјааЮЪОэЕїВщЃЌбЇЩњПЩИљОнздМКЕФЯВКУбЁаовЛУХЃЌРюРЯЪІЖдФГАрШЋАрЭЌбЇЕФбЁПЮЧщПіНјааЭГМЦКѓЃЌжЦГЩСЫСНЗљВЛЭъећЕФЭГМЦЭМ(ШчЭМ).

(1)ИУАрбЇЩњШЫЪ§га ШЫ;
(2)НЋЬѕаЮЭГМЦЭМВЙГфЭъећ;
(3)ШєИУаЃЙВгабЇЩњ3500УћЃЌЧыЙРМЦгаЖрЩйШЫбЁаозуЧђ?
(4)ИУАрАрЮЏ5ШЫжаЃЌ1ШЫбЁаоРКЧђЃЌ3ШЫбЁаозуЧђЃЌ1ШЫбЁаоХХЧђЃЌРюРЯЪІвЊДгет5ШЫжаШЮбЁ2ШЫСЫНтЫћУЧЖдЬхг§бЁаоПЮЕФПДЗЈЃЌЧыФугУСаБэЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓбЁГіЕФ2ШЫЧЁКУ1ШЫбЁаоРКЧђЃЌ1ШЫбЁаозуЧђЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCЪЧЕШБпШ§НЧаЮЃЌвдABЮЊжБОЖзїЁбOЃЌНЛBCБпгкЕуDЃЌНЛACБпгкЕуFЃЌзїDEЁЭACгкЕуEЃЎ
ЃЈ1ЃЉЧѓжЄЃКDEЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєЁїABCЕФБпГЄЮЊ4ЃЌЧѓEFЕФГЄЖШЃЎ
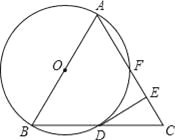
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъМЦЛЎЙКНјAЁЂBСНжжаЭКХЕФЕчЖЏздааГЕЙВ30СОЃЌЦфжаAаЭЕчЖЏздааГЕВЛЩйгк20СОЃЌAЁЂBСНжжаЭКХЕчЖЏздааГЕЕФНјЛѕЕЅМлЗжБ№ЮЊ2500дЊЁЂ3000дЊЃЌЪлМлЗжБ№ЮЊ2800дЊЁЂ3500дЊЃЌЩшИУЩЬЕъМЦЛЎЙКНјAаЭЕчЖЏздааГЕmСОЃЌСНжжаЭКХЕФЕчЖЏздааГЕШЋВПЯњЪлКѓПЩЛёРћШѓyдЊЃЎ
ЃЈ1ЃЉЧѓГіyгыmжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉИУЩЬЕъШчКЮНјЛѕВХФмЛёЕУзюДѓРћШѓЃПДЫЪБзюДѓРћШѓЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com