
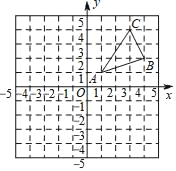
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于原点对称的△A1B1C1;并写出点A1,B1,C1的坐标.
(2)请画出△ABC绕O顺时针旋转90°后的△A2B2C2,并写出点A2,B2,C2的坐标.
科目:初中数学 来源: 题型:
【题目】某校决定对学生感兴趣的球类项目(A:足球,B:篮球,C:排球,D:羽毛球,E:乒乓球)进行问卷调查,学生可根据自己的喜好选修一门,李老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(如图).

(1)该班学生人数有 人;
(2)将条形统计图补充完整;
(3)若该校共有学生3500名,请估计有多少人选修足球?
(4)该班班委5人中,1人选修篮球,3人选修足球,1人选修排球,李老师要从这5人中任选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
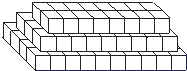
【题目】探索、研究:仪器箱按如图方式堆放(自下而上依次为第1层、第2层、…),受堆放条件限制,堆放时应符合下列条件:每层堆放仪器箱的个数a![]() 与层数n之间满足关系式a
与层数n之间满足关系式a![]() =n32n+247,1n<16,n为整数。
=n32n+247,1n<16,n为整数。
(1)例如,当n=2时,a![]() =232×2+247=187,则a
=232×2+247=187,则a![]() =___,a
=___,a![]() =___;
=___;
(2)第n层比第(n+1)层多堆放多少个仪器箱;(用含n的代数式表示)
(3)假设堆放时上层仪器箱的总重量会对下一层仪器箱产生同样大小的压力,压力单位是牛顿,设每个仪器箱重54 牛顿,每个仪器箱能承受的最大压力为160牛顿,并且堆放时每个仪器箱承受的压力是均匀的。
①若仪器箱仅堆放第1、2两层,求第1层中每个仪器箱承受的平均压力;
②在确保仪器箱不被损坏的情况下,仪器箱最多可以堆放几层?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店计划购进A、B两种型号的电动自行车共30辆,其中A型电动自行车不少于20辆,A、B两种型号电动自行车的进货单价分别为2500元、3000元,售价分别为2800元、3500元,设该商店计划购进A型电动自行车m辆,两种型号的电动自行车全部销售后可获利润y元.
(1)求出y与m之间的函数关系式;
(2)该商店如何进货才能获得最大利润?此时最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数有( )
①已知直角三角形的面积为2,两直角边的比为1:2,则斜边长为![]() ;
;
②直角三角形的最大边长为![]() ,最短边长为1,则另一边长为
,最短边长为1,则另一边长为![]() ;
;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC为直角三角形;
④等腰三角形面积为12,底边上的高为4,则腰长为5.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
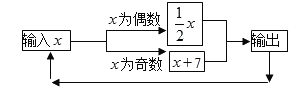
【题目】如图所示的运算程序中,若开始输入的x值为100,我们发现第1次输出的结果为50,第2次输出的结果为25,…,第2018次输出的结果为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(操作发现):如图一,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC的数量关系是 .
(2)(类比探究):如图二,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.
(3)(应用):如图三,将(1)中的矩形ABCD改为正方形,边长AB=4,其它条件不变,求线段GC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中项点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式。请你观察下列儿种简单多面体模型,解答下列问题:

(1)根据上面多面体模型,完成表格中的空格:
多面体 | 项点数(V) | 面数(F) | 棱数(F) |
四面体 | |||
长方体 | |||
正八面体 | |||
正十二面体 |
你发现项点数(V)、面数(F)、棱数(F)之间存在的关系式是__________________________.
(2)一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是 20;
(3)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱,设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com