
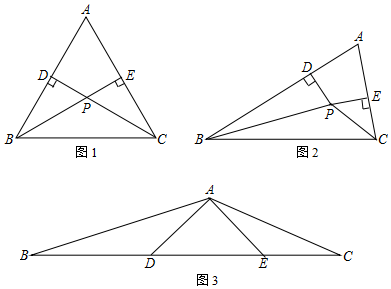
分析 (1)由AAS证明△BDP≌△BFP,得出BD=BF,同理:△CPE≌△CPF,得出CE=CF,即可得出结论;
(2)同(1)得:△BDP≌△BFP,得出∠BPD=∠BPF,BD=BF,证出∠CPF=∠CPE,由AAS证明△CPF≌△CPE,得出CF=CE,即可得出结论;
(3)由三角形内角和定理和等腰直角三角形的性质得出∠ADB=∠CEA=135°,∠BAD=∠C,证出△ABD∽△CAE,得出对应边成比例求出∴$\frac{AD}{CE}=\frac{BD}{AE}$,即AD2=10,再由勾股定理求出DE的长即可.
解答 (1)证明: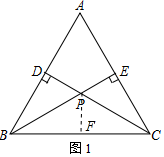 ∵∠BPC=120°,PB=PC,
∵∠BPC=120°,PB=PC,
∴∠PBC=∠PCB=30°,
∵∠A=60°,PD⊥AB,PE⊥AC,
∴∠ABE=∠ACD=30°,∠BPD=∠CPE=60°,
过点P作PF⊥BC于F,如图1所示:
∴∠BPF=∠CPF=60°,
在△BDP和△BFP中,$\left\{\begin{array}{l}{∠BDP=∠BFP=90°}&{\;}\\{∠BPD=∠BPE=60°}&{\;}\\{BP=BP}&{\;}\end{array}\right.$,
∴△BDP≌△BFP(AAS),
∴BD=BF,
同理:△CPE≌△CPF(ASA),
∴CE=CF,
∴BD+CE=BF+CF=BC,
(2)解:仍然成立,理由如下:作PF⊥BC于F,如图2所示:
同(1)得:△BDP≌△BFP,
∴∠BPD=∠BPF,BD=BF,
∵∠A=60°,PD⊥AB,PE⊥AC,
∴∠DOE=120°,
∵∠BPC=120°,
∴∠BPD+∠CPE=120°,
∴∠CPF=∠CPE,
在△CPF和△CPE中,$\left\{\begin{array}{l}{∠PFC=∠PEC=90°}&{\;}\\{∠CPF=∠CPE}&{\;}\\{PC=PC}&{\;}\end{array}\right.$,
∴△CPF≌△CPE(AAS),
∴CF=CE,
∵BF+CF=BC,
∴BD+CE=BC;
(3)解:∵∠BAC=135°,∠DAE=90°,且AD=AE,
∴∠B+∠C=45°,∠ADE=∠AED=45°,
∴∠ADB=∠CEA=135°,
∴∠B+∠BAD=45°,
∴∠BAD=∠C,
∴△ABD∽△CAE,
∴$\frac{AD}{CE}=\frac{BD}{AE}$,
即AD•AE=AD2=BD•CE=5×2=10,
∴DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{20}$=2$\sqrt{5}$;
故答案为:2$\sqrt{5}$.
点评 本题考查了全等三角形的判定与性质、相似三角形的判定与性质、等腰直角三角形的性质、三角形内角和定理等知识;证明三角形全等和三角形相似是解决问题的关键.


科目:初中数学 来源: 题型:解答题
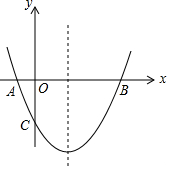 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和C(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和C(0,-5).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )| A. | 点C | B. | 点B | C. | 点A | D. | 点D |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
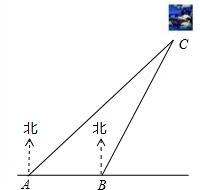 如图,我国某段海防线上有A、B两个观测站,观测站B在观测站A的正东方向上.上午9点,发现海面上C处有一可疑船只,立刻测得该船只在观测站A的北偏东45°方向,在观测站B的北偏东30°的方向上,已知A、C两点之间的距离是50$\sqrt{2}$海里,则此时可疑船只所在C处与观测点B之间的距离是( )
如图,我国某段海防线上有A、B两个观测站,观测站B在观测站A的正东方向上.上午9点,发现海面上C处有一可疑船只,立刻测得该船只在观测站A的北偏东45°方向,在观测站B的北偏东30°的方向上,已知A、C两点之间的距离是50$\sqrt{2}$海里,则此时可疑船只所在C处与观测点B之间的距离是( )| A. | 25$\sqrt{3}$海里 | B. | $\frac{100\sqrt{3}}{3}$海里 | C. | 25海里 | D. | 50海里 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com