
【题目】如图,AB是⊙O的直径,CD是弦,CD⊥AB于点E
(1)求证:△ACE∽△CBE;
(2)若AB=8,设OE=x(0<x<4),CE2=y,请求出y关于x的函数解析式.
【答案】(1)证明:∵AB为圆O的直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵CD⊥AB,
∴∠AEC=∠BEC=90°,
∴∠CAB+∠ACE=90°,
∴∠CBA=∠ACE,
∴△ACE∽△CBE;
(2)解:连接OC,
∵AB=8,∴OC=4,
在Rt△OCE中,OE=x,OC=4,
根据勾股定理得:CE= ![]() ,
,
∵CE2=y,
∴y=﹣x2+16(0<x<4).
【解析】(1)由AB为圆O的直径,利用直径所对的圆周角为直角得到AC与BC垂直,即三角形ABC为直角三角形,利用直角三角形两锐角互余得到一对角互余,再由CD与AB垂直,得到三角形ACE与三角形BCE都为直角三角形,同理得到一对角互余,等量代换得到一对角相等,再由一对直角相等,利用两对对应角相等的两三角形相似即可得证;
(2)连接OC,由AB垂直于CD,在直角三角形OCE中,由OE=x,OC=4,利用勾股定理表示出CE,代入CE2=y中,即可得到y关于x的函数解析式.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


科目:初中数学 来源: 题型:
【题目】一个口袋中有1个黑球和若干个白球,这些球除颜色外其他都相同.已知从中任意摸取一个球,摸得黑球的概率为![]() .
.
(1)求口袋中白球的个数;
(2)如果先随机从口袋中摸出一球,不放回,然后再摸出一球,求两次摸出的球都是白球的概率.用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A,B在数轴上对应的数分别用a,b表示,且(![]() ab+100)2+|a﹣20|=0,P是数轴上的一个动点.
ab+100)2+|a﹣20|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离.
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数.
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度第四次向右移动7个单位长度,….点P能移动到与A或B重合的位置吗?若都不能,请直接回答.若能,请直接指出,第几次移动与哪一点重合?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】读题画图计算并作答
画线段AB=3 cm,在线段AB上取一点K,使AK=BK,在线段AB的延长线上取一点C,使AC=3BC,在线段BA的延长线取一点D,使AD=![]() AB.
AB.
(1)求线段BC、DC的长?
(2)点K是哪些线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
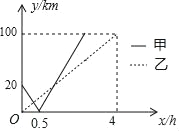
【题目】沿河岸有A,B,C三个港口,甲乙两船同时分别从AB港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:
①乙船的速度是25km/h;②从A港到C港全程为120km;③甲船比乙船早1.5小时到达终点;④若设图中两者相遇的交点为P点,P点的坐标为(![]() ,
,![]() );⑤如果两船相距小于10km能够相互望见,那么甲、乙两船可以相互望见时,x的取值范围是
);⑤如果两船相距小于10km能够相互望见,那么甲、乙两船可以相互望见时,x的取值范围是![]() <x<2.其中正确的结论有_____.
<x<2.其中正确的结论有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线 ![]() ,
, ![]() ,点P为双曲线
,点P为双曲线 ![]() 上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线
上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别依次交双曲线 ![]() 于D、C两点,则△PCD的面积为 .
于D、C两点,则△PCD的面积为 . 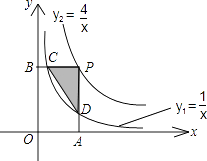
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com