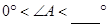练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【小题1】如图1，在矩形ABCD中，AB=2BC，M是AB的中点．直接写出∠BMD与∠ADM的倍数关系；
    【小题2】如图2，若四边形ABCD是平行四边形， AB=2BC，M是AB的中点，过C作CE⊥AD与AD所在直线交于点E．
    ①若∠A为锐角，则∠BME与∠AEM有怎样的倍数关系，并证明你的结论；
    ②当时，上述结论成立；
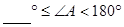    当 时，上述结论不成立．

    【小题1】∠BMD= 3 ∠ADM
    【小题2】见解析有。
    当0°<∠A<120°时，结论成立；
    当时，结论不成立.解析:
    （1）∠BMD= 3 ∠ADM                          ………… 2分
    （2）联结CM，取CE的中点F，联结MF，交DC于N

    ∵M是AB的中点，∴MF∥AE∥BC，
    ∴∠AEM=∠1，∠2=∠4，   ……… 3分
    ∵AB=2BC，∴BM=BC，∴∠3=∠4.            
    ∵CE⊥AE，∴MF⊥EC，又∵F是EC的中点，
    ∴ME=MC，∴∠1=∠2.    ……….4分
    ∴∠1=∠2=∠3.
    ∴∠BME =3∠AEM.        ………. 5分
    （3）当0°<∠A<120°时，结论成立；
    当时，结论不成立.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


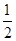    【小题1】如图25-1，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是边BC、CD上的点，且∠EAF=∠BAD.求证:EF＝BE＋FD;
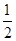    【小题2】如图25-2在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD上的点，且∠EAF=∠BAD, (1)中的结论是否仍然成立？不用证明.
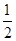    【小题3】如图25-3在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E、F分别是边BC、CD延长线上的点，且∠EAF=∠BAD, (1)中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明.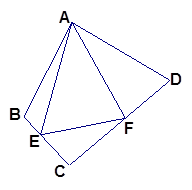

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式，这种解决问题的方法我们称之为面积法．
    【小题1】如图1，在等腰三角形ABC中，AB=AC，AC边上的高为，M是底边BC上的任意一点，点M到腰AB、AC的距离分别为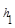、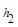．连接AM,可得结论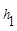+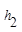=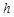．当点M在BC延长线上时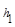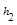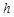，、、之间的等量关系式是               ．（直接写出结论不必证明）．

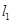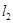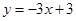    【小题2】应用：平面直角坐标系中有两条直线：、：，若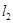上的一点M到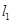的距离是1．请运用（1）的条件和结论求出点M的坐标．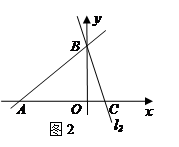

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年安徽省马鞍山六中中考模拟数学卷 题型：解答题

    三角形中，顶角等于36°的等腰三角形称为黄金三角形，如图1，在△ABC中，已知：AB＝AC，且∠A＝36°．

    【小题1】在图1中，用尺规作AB的垂直平分线交AC于D，并连接BD（保留作图痕迹，不写作法）；
    【小题2】△BCD是不是黄金三角形，如果是，请给出证明；如果不是，请说明理由；
    【小题3】设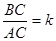，试求k的值；
    【小题4】如图2，在△A1B1C1中，已知A1B1＝A1C1，∠A1＝108°，且A1B1＝AB，
    请直接写出的值．

    查看答案和解析>>

    科目：初中数学 来源：2012届北京昌平区中考模拟数学题卷 题型：解答题


    【小题1】如图25-1，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是边BC、CD上的点，且∠EAF=∠BAD.求证:EF＝BE＋FD;
    【小题2】如图25-2在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD上的点，且∠EAF=∠BAD, (1)中的结论是否仍然成立？不用证明.
    【小题3】如图25-3在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E、F分别是边BC、CD延长线上的点，且∠EAF=∠BAD, (1)中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明.

    查看答案和解析>>

    同步练习册答案