
【题目】已知二次函数y=x -2mx(m为常数),当-1≤x≤2时,函数y的最小值为-2,则m的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D. -
D. -![]() 或
或![]()
【答案】D
【解析】先将二次函数配方得: ![]() ,根据二次函数图象和性质可知:
,根据二次函数图象和性质可知:
对称轴![]() ,由于对称轴位置不确定,所以分m<-1, m>2, -1≤m≤2三种情况,根据二次函数y的最小值为-2,结合二次函数图象和性质进行解答, ①若m<-1,当x=-1时,y最小值=1+2m=-2,解得m=-
,由于对称轴位置不确定,所以分m<-1, m>2, -1≤m≤2三种情况,根据二次函数y的最小值为-2,结合二次函数图象和性质进行解答, ①若m<-1,当x=-1时,y最小值=1+2m=-2,解得m=-![]() ,②若m>2,当x=2时,y最小值=4-4m=-2,解得m=
,②若m>2,当x=2时,y最小值=4-4m=-2,解得m=![]() <2(舍),
<2(舍),
③若-1≤m≤2,当x=m时,y最小值=-![]() =-2,解得m=
=-2,解得m=![]() 或m=-
或m=-![]() <-1(舍),综上所述,m的值为-
<-1(舍),综上所述,m的值为-![]() 或
或![]() ,因此正确选项是D.
,因此正确选项是D.
y=x -2mx=(x-m) -m2.分以下3种情况:①若m<-1,当x=-1时,y最小值=1+2m=-2,解得m=-![]() ;②若m>2,当x=2时,y最小值=4-4m=-2,解得m=
;②若m>2,当x=2时,y最小值=4-4m=-2,解得m=![]() <2(舍);③若-1≤m≤2,当x=m时,y最小值=-m2=-2,解得m=
<2(舍);③若-1≤m≤2,当x=m时,y最小值=-m2=-2,解得m=![]() 或m=-
或m=-![]() <-1(舍).综上所述,m的值为-
<-1(舍).综上所述,m的值为-![]() 或
或![]() ,故选D
,故选D


科目:初中数学 来源: 题型:
【题目】如图①,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图②.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
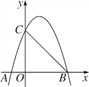
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别交于A(-1,0)、B(3,0)、C(0,3)三点.
(1)试求抛物线的解析式;
(2)P是直线BC上方的抛物线上的一个动点,设P的横坐标为t,P到BC的距离为h,求h与t的函数关系式,并求出h的最大值;
(3)设点M是x轴上的动点,在平面直角坐标系中,是否存在点N,使得以点A、C、M、N为顶点的四边形是菱形?若存在,求出所有符合条件的点N坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
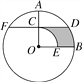
【题目】(2016·新疆中考)如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作弧CE,交OB于E点.
,以O为圆心,OC为半径作弧CE,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组为了解我市气温变化情况,记录了今年1月份连续6天的最低气温(单位:℃):﹣7,﹣4,﹣2,1,﹣2,2.关于这组数据,下列结论不正确的是( )
A.平均数是﹣2
B.中位数是﹣2
C.众数是﹣2
D.方差是7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题: 某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个,已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润20000元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com