
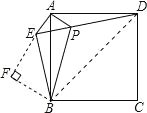
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )

A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
【答案】D.
【解析】
试题解析:①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,
∴∠EAB=∠PAD,
又∵AE=AP,AB=AD,
∴△APD≌△AEB(故①正确);
③∵△APD≌△AEB,
∴∠APD=∠AEB,
又∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,
∴∠BEP=∠PAE=90°,
∴EB⊥ED(故③正确);
②过B作BF⊥AE,交AE的延长线于F,
∵AE=AP,∠EAP=90°,
∴∠AEP=∠APE=45°,
又∵③中EB⊥ED,BF⊥AF,
∴∠FEB=∠FBE=45°,
又∵BE=![]() ,
,
∴BF=EF=![]() (故②不正确);
(故②不正确);
④如图,连接BD,在Rt△AEP中,
∵AE=AP=1,
∴EP=![]() ,
,
又∵PB=![]() ,
,
∴BE=![]() ,
,
∵△APD≌△AEB,
∴PD=BE=![]() ,
,
∴S△ABP+S△ADP=S△ABD-S△BDP=![]() S正方形ABCD-
S正方形ABCD-![]() ×DP×BE
×DP×BE
=![]() ×(4+
×(4+![]() )-
)-![]() ×
×![]() ×
×![]()
=![]() +
+![]() .(故④不正确).
.(故④不正确).
⑤∵EF=BF=![]() ,AE=1,
,AE=1,
∴在Rt△ABF中,AB2=(AE+EF)2+BF2=4+![]() ,
,
∴S正方形ABCD=AB2=4+![]() (故⑤正确);
(故⑤正确);
故选D.


科目:初中数学 来源: 题型:
【题目】某班分组去两处植树,第一组26人,第二组22人.现第一组在植树中遇到困难,需第二组支援.问第二组调多少人去第一组,才能使第一组的人数是第二组的3倍?设从第二组抽调x人,则可列方程为( )
A.26+x=3×26
B.26=3(22﹣x)
C.3(26+x)=22﹣x
D.26+x=3(22﹣x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.现要把它加工成矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB,AC上.
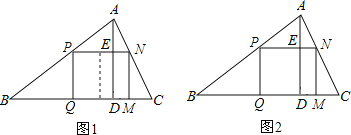
(1)如果此矩形可分割成两个并排放置的正方形,如图1,此时,这个矩形零件的两条邻边长分别为多少mm?请你计算.
(2)如果题中所要加工的零件只是矩形,如图2,这样,此矩形零件的两条邻边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条邻边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
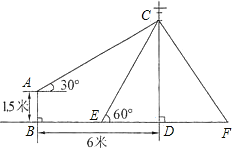
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,矩形ABCD的对角线相交于点O,
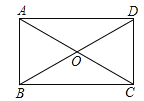
(1)若AB=2,∠AOD=120,求对角线AC的长;
(2)若AC=2AB.求证:△AOB是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G是边长为8的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=10.

(1)求FG的长;
(2)直接写出图中与△BHG相似的所有三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com