
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做等对角四边形.请解决下列问题: 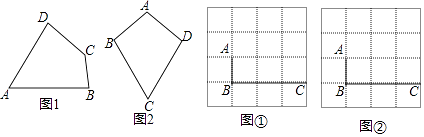
(1)已知:如图1,四边形ABCD是等对角四边形,∠A≠∠C,∠A=70°,∠B=75°,则∠C=°,∠D=°
(2)在探究等对角四边形性质时: 小红画了一个如图2所示的等对角四边形ABCD,其中,∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立,请你证明该结论;
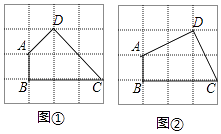
(3)图①、图②均为4×4的正方形网格,线段AB、BC的端点均在网点上.按要求在图①、图②中以AB和BC为边各画一个等对角四边形ABCD. 要求:四边形ABCD的顶点D在格点上,所画的两个四边形不全等.
(4)已知:在等对角四边形ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4,求对角线AC的长.
【答案】
(1)140;75
(2)证明:如图2,连接BD,
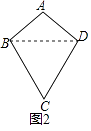
∵AB=AD,
∴∠ABD=∠ADB,
∵∠ABC=∠ADC,
∴∠ABC﹣∠ABD=∠ADC﹣∠ADB,
∴∠CBD=∠CDB,
∴CB=CD;
(3)如图所示:
(4)解:分两种情况:
①当∠ADC=∠ABC=90°时,延长AD,BC相交于点E,如图3所示:
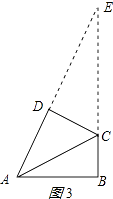
∵∠ABC=90°,∠DAB=60°,AB=5,
∴∠E=30°,
∴AE=2AB=10,
∴DE=AE﹣AD=10﹣4═6,
∵∠EDC=90°,∠E=30°,
∴CD=2 ![]() ,
,
∴AC= ![]() =
= ![]() =2
=2 ![]() ;
;
②当∠BCD=∠DAB=60°时,
过点D作DM⊥AB于点M,DN⊥BC于点N,如图4所示:
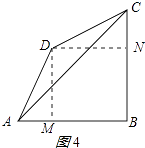
则∠AMD=90°,四边形BNDM是矩形,
∵∠DAB=60°,
∴∠ADM=30°,
∴AM= ![]() AD=2,
AD=2,
∴DM=2 ![]() ,
,
∴BM=AB﹣AM=5﹣2=3,
∵四边形BNDM是矩形,
∴DN=BM=3,BN=DM=2 ![]() ,
,
∵∠BCD=60°,
∴CN= ![]() ,
,
∴BC=CN+BN=3 ![]() ,
,
∴AC= ![]() =2
=2 ![]() .
.
综上所述:AC的长为2 ![]() 或2
或2 ![]() .
.
故答案为:140,75.
【解析】(1)解:∵四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=75°, ∴∠D=∠B=75°,
∴∠C=360°﹣75°﹣75°﹣70°=140°;
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握勾股定理的逆定理(如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形)的相关知识才是答题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的顶点B在反比例函数 ![]() 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( )
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( ) 
A.12
B.4 ![]()
C.12-3 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF. 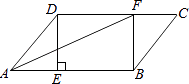
(1)求证:四边形DEBF是矩形;
(2)若AF平分∠DAB,AE=3,BF=4,求ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,拦水坝的横断面为梯形ABCD,AB∥CD,坝顶宽DC为6米,坝高DG为2米,迎水坡BC的坡角为30°,坝底宽AB为(8+2 ![]() )米.
)米. 
(1)求背水坡AD的坡度;
(2)为了加固拦水坝,需将水坝加高2米,并且保持坝顶宽度不变,迎水坡和背水坡的坡度也不变,求加高后坝底HB的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”小长假,小颖和小梅两家计划从“北京天安门”“三亚南山”“内蒙古大草原”三个景区中任意选择一景区游玩,小颖和小梅制作了如下三张质地大小完全相同的卡片,背面朝上洗匀后各自从中抽去一张来确定游玩景区(第一人抽完放回洗匀后另一人再抽去),则两人抽到同一景区的概率是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)连接DE,BF,若BD⊥EF,试探究四边形EBFD的形状,并对结论给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹): 
(1)作△ABC的外心O;
(2)设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC和AC上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com