
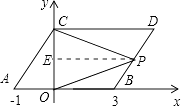
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ����1��0������3��0������ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD�� 
��1�����C��D�����꼰�ı���ABDC�����S�ı���ABDC��
��2����y�����Ƿ����һ��P������PA��PB��ʹS��PAB=S�ı���ABDC������������һ�㣬�����P�����ꣻ�������ڣ���˵�����ɣ�
��3����P���߶�BD�ϵ�һ�����㣬����PC��PO������P��BD���ƶ�ʱ������B��D�غϣ��������н��ۣ� �� ![]() ��ֵ���䣬��
��ֵ���䣬�� ![]() ��ֵ���䣬��������ֻ��һ������ȷ�ģ������ҳ�������۲�����ֵ��
��ֵ���䣬��������ֻ��һ������ȷ�ģ������ҳ�������۲�����ֵ��
���𰸡�
��1���⣺�����⣬��C��0��2����D��4��2����
��S�ı���ABDC=AB��OC=4��2=8��
��2�����ڣ�
���P��AB�ľ���Ϊh��
S��PAB= ![]() ��AB��h=2h��
��AB��h=2h��
��S��PAB=S�ı���ABDC����2h=8�����h=4��
��P��0��4����0����4����
��3�����ۢ���ȷ��
��P����PE��AB��OC��E�㣬
��AB��PE��CD��
���DCP+��BOP=��CPE+��OPE=��CPO��
�� ![]() =1��
=1��
����������1������ƽ�ƹ��ɣ�ֱ�ӵó���C��D�����꣬���ݣ��ı���ABDC�����=AB��OC��⣻��2�����ڣ����P��AB�ľ���Ϊh����S��PAB= ![]() ��AB��h������S��PAB=S�ı���ABDC �� �з�����h��ֵ��ȷ��P�����ꣻ��3�����ۢ���ȷ����P����PE��AB��OC��E�㣬����ƽ���ߵ����ʵá�DCP+��BOP=��CPE+��OPE=��CPO���ʱ�ֵΪ1��
��AB��h������S��PAB=S�ı���ABDC �� �з�����h��ֵ��ȷ��P�����ꣻ��3�����ۢ���ȷ����P����PE��AB��OC��E�㣬����ƽ���ߵ����ʵá�DCP+��BOP=��CPE+��OPE=��CPO���ʱ�ֵΪ1��
�����㾫����������Ŀ����֪����������ƽ���ߵ����ʺ������ε���������֪ʶ���Եõ�����Ĵ𰸣���Ҫ������ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У��ڴ�����ȣ���ֱ��ƽ�У�ͬ���ڽǻ����������ε����=1/2���ס��ߣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC��ֱ�������Σ��ҡ�C=Rt�ϣ�����A=34�㣬���B=��������
A.66��
B.56��
C.46��
D.146��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һԪ���η���(1+x)(x+3)=2x2+1����һ����ʽ��:__________________�����Ķ�����ϵ����_________��һ����ϵ����________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ������������ǵ�ƽ�����ཻ�õ��Ķ۽�Ϊ��������
A.150o
B.135o
C.120o
D.120o��135o
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ���������֣�������⣺ ���֪�� ![]() ������������������������ѭ��С�������
������������������������ѭ��С������� ![]() ��С���������Dz�����ȫ����д����������С����
��С���������Dz�����ȫ����д����������С���� ![]() ��1����ʾ
��1����ʾ ![]() ��С�����֣���ͬ��С���ı�ʾ������
��С�����֣���ͬ��С���ı�ʾ������
��ʵ�ϣ�С���ı�ʾ�������е�������Ϊ ![]() ������������1�����������ȥ���������֣������С�����֣�
������������1�����������ȥ���������֣������С�����֣�
�����磺
�� ![]() ��
�� ![]() ��
�� ![]() ����2��
����2�� ![]() ��3��
��3��
�� ![]() ����������Ϊ2��С������Ϊ��
����������Ϊ2��С������Ϊ�� ![]() ��2����
��2����
����
��1��![]() ������������ �� �������� ��
������������ �� �������� ��
��2����� ![]() ��С������Ϊa��
��С������Ϊa�� ![]() ����������Ϊb����a+b��
����������Ϊb����a+b�� ![]() ��ֵ��
��ֵ��
��3����֪��10+ ![]() =x+y������x����������0��y��1����x��y���෴����
=x+y������x����������0��y��1����x��y���෴����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A���һ�κ�����ͼ��������������y=2x��ͼ���ཻ�ڵ�B �� �����һ�κ����Ľ���ʽ�ǣ�������.
A.y=2x+3
B.y=x-3
C.y=2x-3
D.y=-x+3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ABCƽ�ƺ�õ���DEF��
��1������A=80�㣬��E=60�㣬���C�Ķ�����
��2����AC=BC��BC��DF�ཻ�ڵ�O����OD��OB�����˵�����ɣ�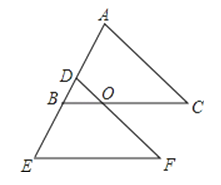
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A��2����1���ڣ� ��
A.��һ����
B.�ڶ�����
C.��������
D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������˶�Ա������ͬ����¸����10����������ƽ��������8������ֱ�Ϊ4��2.2����ɼ��Ϻõ���__________________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com