练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】改革开放以来，人们的支付方式发生了巨大转变，近年来，移动支付已成为主要的支付方式之一，为了解某校学生上个月两种移动支付方式的使用情况，从全校名学生中随机抽取了人，发现样本中两种支付方式都不使用的有人，样本中仅使用种支付方式和仅使用种支付方式的学生的支付金额(元)的分布情况如下：

    支付金额（元）

    支付方式

    仅使用

    人

    人

    人

    仅使用

    人

    人

    人

    下面有四个推断：

    ①从样本中使用移动支付的学生中随机抽取一名学生，该生使用A支付方式的概率大于他使用B支付方式的概率；

    ②根据样本数据估计，全校1000名学生中．同时使用A、B两种支付方式的大约有400人；

    ③样本中仅使用A种支付方式的同学，上个月的支付金额的中位数一定不超过1000元；

    ④样本中仅使用B种支付方式的同学，上个月的支付金额的平均数一定不低于1000元．其中合理的是（ ）

    A.①③B.②④C.①②③D.①②③④

    【答案】C

    【解析】

    由题意根据概率公式、样本估计总体思想的运用、中位数和平均数的定义逐一判断可得．

    解：①从样本中使用移动支付的学生中随机抽取一名学生，该生使用A支付方式的概率为

    ，使用B支付方式的概率为，此推断合理；

    ②根据样本数据估计，全校1000名学生中，同时使用A，B两种支付方式的大约有（人），此推断合理；

    ③样本中仅使用A种支付方式的同学，第15、16个数据均落在0＜a≤1000，所以上个月的支付金额的中位数一定不超过1000元，此推断合理；

    ④样本中仅使用B种支付方式的同学，上个月的支付金额的平均数无法估计，此推断不正确．

    故推断正确的有①②③.

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，在中，，点从点出发以的速度沿折线运动，点从点出发以的速度沿运动，，两点同时出发，当某一点运动到点时，两点同时停止运动.设运动时间为，的面积为，关于的函数图像由，两段组成，如图2所示.

    （1）求的值；

    （2）求图2中图像段的函数表达式；

    （3）当点运动到线段上某一段时的面积，大于当点在线段上任意一点时的面积，求的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点M是⊙O直径AB上一定点，点C是直径AB上一个动点，过点作交⊙O于点，作射线DM交⊙O于点N，连接BD．

    小勇根据学习函数的经验，对线段AC，BD，MN的长度之间的数量关系进行了探究．

    下面是小勇的探究过程，请补充完整：

    （1）对于点C在AB的不同位置，画图，测量，得到了线段AC，BD，MN的长度的几组值，如下表：

    位置1

    位置2

    位置3

    位置4

    位置5

    位置6

    位置7

    AC/cm

    0．00

    1．00

    2．00

    3．00

    4．00

    5．00

    6．00

    BD/cm

    6．00

    5．48

    4．90

    4．24

    3．46

    2．45

    0．00

    MN/cm

    4．00

    3．27

    2．83

    2．53

    2．31

    2．14

    2．00

    在AC，BD，MN的长度这三个量中，如果选择________的长度为自变量，那么________的长度和________的长度为这个自变量的函数；

    （2）在同一平面直角坐标系xOy中，画出（1）中确定的函数的图象；

    （3）结合函数图象解决问题：当BD=MN时，线段AC的长度约为_____cm（结果精确到0.1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班甲、乙、丙三名同学20天的体温数据记录如下表：

    甲的体温

    乙的体温

    丙的体温

    温度（℃）

    36.1

    36.4

    36.5

    36.8

    温度（℃）

    36.1

    36.4

    36.5

    36.8

    温度（℃）

    36.1

    36.4

    36.5

    36.8

    频数

    5

    5

    5

    5

    频数

    6

    4

    4

    6

    频数

    4

    6

    6

    4

    则在这20天中，甲、乙、丙三名同学的体温情况最稳定的是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：在平面直角坐标系中，对于任意的实数，直线都经过平面内一个定点．

    （1）求点的坐标．

    （2）反比例函数的图象与直线交于点和另外一点

    ①求的值；

    ②当时，求的取值范围

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：关于的方程有实数根．

    (1)求的取值范围；

    (2)若该方程有两个实数根，取一个的值，求此时该方程的根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知线段AB，过点A的射线l⊥AB．在射线l上截取线段AC＝AB，连接BC，点M为BC的中点，点P为AB边上一动点，点N为线段BM上一动点，以点P为旋转中心，将△BPN逆时针旋转90°得到△DPE，B的对应点为D，N的对应点为E．

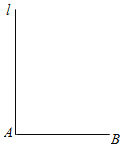
    （1）当点N与点M重合，且点P不是AB中点时，

    ①据题意在图中补全图形；

    ②证明：以A，M，E，D为顶点的四边形是矩形．

    （2）连接EM．若AB＝4，从下列3个条件中选择1个：

    ①BP＝1，②PN＝1，③BN＝，

    当条件　 （填入序号）满足时，一定有EM＝EA，并证明这个结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在四边形ABCD中，用①AB∥DC，②AD＝BC，③∠A＝∠C中的两个作为题设，余下的一个作为结论．用“如果…，那么…“的形式，写出一个真命题：在四边形ABCD中，_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

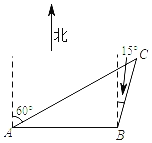
    【题目】在一次综合社会实践活动中，小东同学从A处出发，要到A地北偏东60°方向的C处，他先沿正东方向走了4千米到达B处，再沿北偏东15°方向走，恰能到达目的地C，如图所示，则A、C两地相距__千米．（结果精确到0.1千米，参考数据：≈1.414，≈1.732）

    查看答案和解析>>

    同步练习册答案