
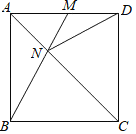
【题目】如图所示,在正方形ABCD中,AD=6,M在AD上从A向D运动,连接BM交AC于N,连接DN.
(1)证明:无论M运动到AD上的何处,都有△ABN≌△ADN;
(2)当M运动到何处时,S△ABN=![]() S正方形ABCD?
S正方形ABCD?
(3)若M从A到D,再从D到C,在整个运动过程中,DM为多少时,△ABN是等腰三角形?
【答案】(1)见解析;(2)AM=2时;(3)当DM=0或6或12﹣6![]() 时,△ABN是等腰三角形
时,△ABN是等腰三角形
【解析】
(1)由正方形的性质得出AB=AD=BC=6,∠BAN=∠DAN,AD∥BC,由SAS证明△ABN≌△ADN即可;
(2)由正方形的性质得出![]() ,得出
,得出![]() ,由平行线得出△AMN∽△CBN,得出
,由平行线得出△AMN∽△CBN,得出![]() ,求出
,求出![]() ;
;
(3)分三种情况:①若AN=BN,此时M与D重合,DM=0;
②若AB=BN,此时M与重合,DM=6;
③若AB=AN,此时点M在DC上,由平行线得出△ABN∽△CMN,得出CM=CN,求出![]() ,即可得出
,即可得出![]() .
.
(1)证明:∵四边形ABD是正方形
∴AB=AD=BC=6,∠BAN=∠DAN,AD∥BC
在△ABN和△ADN中,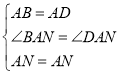
![]() ;
;
(2)![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
![]()
∵AM∥BC
∴△AMN∽△CBN
![]()
![]()
即当AM=2时,![]() ;
;
(3)若△ABN是等腰三角形,分三种情况:
①若AN=BN,此时M与D重合,DM=0
②若AB=BN,此时M与重合,DM=6
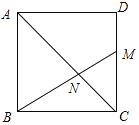
③若AB=AN,此时点M在DC上,如图所示:
∵AB∥CM
∴△ABN∽△CMN
∴![]()
∴CM=CN
![]()
![]()
![]()
综上,当DM=0或6或![]() 时,△ABN是等腰三角形.
时,△ABN是等腰三角形.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老王面前有两个容积相同的杯子,杯子甲他装了三分之一的葡萄酒,杯子乙他装了半杯的王老吉凉茶,老张过来将装有凉茶的杯子乙倒满了酒,老王又将杯子乙中饮料倒一部分到杯子甲,使得两个杯子的饮料分量相同.然后老王让老张先选一杯一起喝了,如果老张不想多喝酒,那么他应该选择( )
A.甲杯B.乙杯C.甲、乙是一样的D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
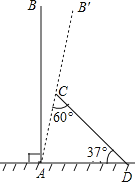
【题目】某次台风来袭时,一棵笔直大树树干AB(假定树干AB垂直于水平地面)被刮倾斜7°(即∠BAB′=7°)后折断倒在地上,树的顶部恰好接触到地面D处,测得∠CDA=37°,AD=5米,求这棵大树AB的高度.(结果保留根号)(参考数据:sin37≈0.6,cos37=0.8,tan37≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC内接于⊙O,AC是直径,D在⊙O上,且AC平分∠BCD,AE∥BC,交CD于E,F在CD的延长线上,且AE=EF.连接AF
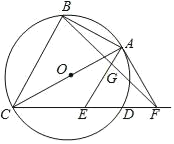
(1)求证:AF是⊙O的切线;
(2)连接BF交AE于G,若AB=12,AE=13,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
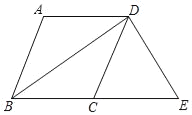
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划根据学生的兴趣爱好组建课外兴趣小组,并随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
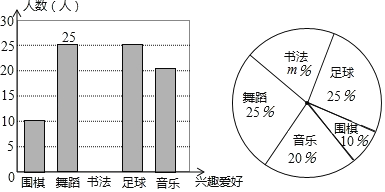
![]() 学校这次调查共抽取了 名学生;
学校这次调查共抽取了 名学生;
![]() 求
求![]() 的值并补全条形统计图;
的值并补全条形统计图;
![]() 在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
在扇形统计图中,“围棋”所在扇形的圆心角度数为 ;
![]() 设该校共有学生
设该校共有学生![]() 名,请你估计该校有多少名学生喜欢足球.
名,请你估计该校有多少名学生喜欢足球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD⊥DC于D,且AC平分∠DAB.延长DC交AB的延长线于点P.
(1)求证:PC2=PAPB;
(2)若3AC=4BC,⊙O的直径为7,求线段PC的长.
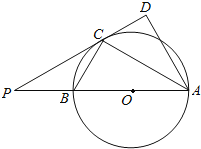
查看答案和解析>>
科目:初中数学 来源: 题型:
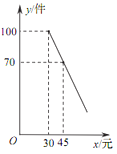
【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com