
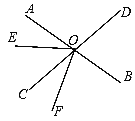
【题目】如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度数;
(2)若OF平分∠BOE,问:OB是∠DOF的平分线吗?试说明理由.
【答案】(1) 30°;(2) OB是∠DOF的平分线,理由见解析
【解析】
(1)设∠AOE=2x,根据对顶角相等求出∠AOC的度数,根据题意列出方程,解方程即可;
(2)根据角平分线的定义求出∠BOF的度数即可.
(1)∵∠AOE:∠EOC=2:3.∴设∠AOE=2x,则∠EOC=3x,∴∠AOC=5x.
∵∠AOC=∠BOD=75°,∴5x=75°,解得:x=15°,则2x=30°,∴∠AOE=30°;
(2)OB是∠DOF的平分线.理由如下:
∵∠AOE=30°,∴∠BOE=180°﹣∠AOE=150°.
∵OF平分∠BOE,∴∠BOF=75°.
∵∠BOD=75°,∴∠BOD=∠BOF,∴OB是∠DOF的角平分线.


科目:初中数学 来源: 题型:
【题目】某学校为了推动球类运动的普及,成立多个球类运动社团,为此,学生会采取抽样调查的方法,从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好(要求每位同学只能选择其中一种自己喜欢的球类运动),并将调查结果绘制成了如下条形统计图和扇形统计图(不完整).请你根据图中提供的信息,解答下列问题:

(1)本次抽样调查,共调查了 名学生;
(2)请将条形统计图和扇形统计图补充完整;
(3)若该学校共有学生1800人,根据以上数据分析,试估计选择排球运动的同学约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠A=30°,∠B=60°. 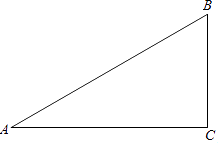
(1)作∠B的平分线BD,交AC于点D;作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(2)连接DE,求证:△ADE≌△BDE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班有学生55人,其中男生与女生的人数之比为6:5.
(1)求出该班男生与女生的人数;
(2)学校要从该班选出20人参加学校的合唱团,要求:①男生人数不少于7人;②女生人数超过男生人数2人以上.请问男、女生人数有几种选择方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(﹣2,0)、B(0,1)、C(d,2).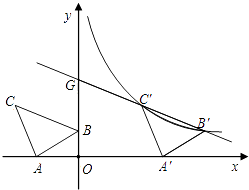
(1)求d的值;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图象上.请求出这个反比例函数和此时的直线B′C′的解析式;
(3)在(2)的条件下,直线BC交y轴于点G.问是否存在x轴上的点M和反比例函数图象上的点P,使得四边形PGMC′是平行四边形?如果存在,请求出点M和点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为54°,已知坡角为30°,你能求出楼房AB的高度吗?(tan54°≈1.38,结果精确到0.1m)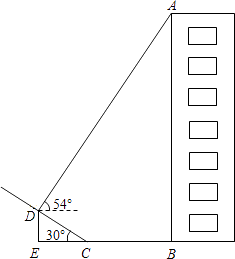
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在开展 “校园献爱心”活动中,准备向南部山区学校捐赠男、女两种款式的书包.已知男款书包的单价50元/个,女款书包的单价70元/个.
(1)原计划募捐3400元,购买两种款式的书包共60个,那么这两种款式的书包各买多少个?
(2)在捐款活动中,由于学生捐款的积极性高涨,实际共捐款4800元,如果至少购买两种款式的书包共80个,那么女款书包最多能买多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一组有规律的图案,它们是由边长相同的正方形和正三角形拼接而成,第①个图案有4个三角形和1个正方形,第②个图案有7个三角形和2个正方形,第③个图案有10个三角形和3个正方形,…依此规律,第n个图案有 ____________个三角形(用含n的代数式表示);

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com