练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．若$\frac{1-3x}{{x}^{2}-1}$=$\frac{M}{x+1}$+$\frac{N}{x-1}$，求M，N的值．

    分析 已知等式右边通分并利用同分母分式的加法法则计算，再利用分式相等的条件求出M与N的值即可．

    解答 解：已知等式整理得：$\frac{1-3x}{{x}^{2}-1}$=$\frac{M（x-1）+N（x+1）}{{x}^{2}-1}$，
    可得1-3x=（M+N）x+N-M，即$\left\{\begin{array}{l}{M+N=-3}\\{N-M=1}\end{array}\right.$，
    解得：$\left\{\begin{array}{l}{M=-2}\\{N=-1}\end{array}\right.$．

    点评 此题考查了分式的加减法，以及分式相等的条件，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

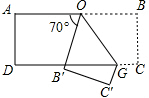    15．如图，把一张长方形的纸按如图所示那样折叠，B、C两点分别落在B′，C′点处，若∠AOB′=70°，则∠B′OG的度数为（　　）
    A．50°B．55°C．60°D．65°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．下列命题是真命题的有：①若a＞b，则a2＞b2；②三角形一边上的中点到另外两边的距离相等；③若一个三角形一边的中线等于这边的一半，那么这个三角形是直角三角形；④同位角相等；⑤“作两条相交的直线”这句话是一个命题．（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如图，已知AC⊥BC，CD⊥AB，AC=3，BC=4，CD=2.4，则点C到直线AB的距离等于2.4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如果点P（x2-4，y+1）是坐标原点，求代数式2x+y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．当x=-1时，求$\frac{{x}^{2}-x-6}{x-3}$÷$\frac{x+3}{{x}^{2}+x-6}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

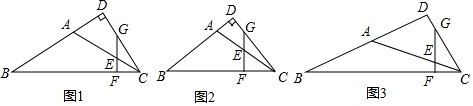
    17．如图，是将两个边长分别为和的正方形拼在一起，B、C、G三点在同一直线上．连接BD和BF，若两正方形的边长满足a+b=6，ab=6，你能求出阴影部分的面积S阴吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如果二次函数y=x2-6x+8在x的一定取值范围内有最大值（或最小值）为3，满足条件的x的取值范围可以是（　　）
    A．-1≤x≤5B．1≤x≤6C．-2≤x≤4D．-1≤x≤1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．在△ABC中，AB=AC，CD⊥AB于D，E为AC上一点，EF⊥BC于F，交CD于G

    （1）如图1，若∠BAC=120°，求证：CG=$\sqrt{3}$EG；
    （2）如图2，点E为AC的中点，若BF=6$\sqrt{2}$，CG=5，求DG的长；
    （3）如图3，若EG=$\sqrt{2}$CF，直接写出$\frac{AD}{AB}$的值．

    查看答案和解析>>

    同步练习册答案