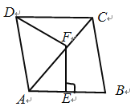
【题目】如图，菱形
的边
的垂直平分线交于点
，交
于点
，连接
．当
时，则
（ ）
A.
B.
C.
D.
【答案】B
【解析】
连接BF，根据菱形的对角线平分一组对角线可得∠BAC=50°，根据线段垂直平分线上的点到两端点的距离相等可得AF=BF，根据等边对等角可得∠FBA=∠FAB，再根据菱形的邻角互补求出∠ABC，然后求出∠CBF，最后根据菱形的对称性可得∠CDF=∠CBF．
解：如图，连接BF，
在菱形ABCD中，∠BAC=
∠BAD=×100°=50°，
∵EF是AB的垂直平分线，
∴AF=BF，
∴∠FBA=∠FAB=50°，
∵菱形ABCD的对边AD∥BC，
∴∠ABC=180°-∠BAD=180°-100°=80°，
∴∠CBF=∠ABC-∠ABF=80°-50°=30°，
由菱形的对称性，∠CDF=∠CBF=30°．
故选：B．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy内有三点：（0，﹣2），（1，﹣1），（2.17，0.37）．则过这三个点_____（填“能”或“不能”）画一个圆，理由是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
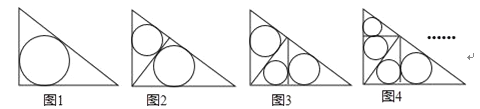
【题目】如图1～4，在直角边分别为3和4的直角三角形中，每多作一条斜边上的高就增加一个三角形的内切圆，依此类推，图10中有10个直角三角形的内切圆，它们的面积分别记为S1，S2，S3，…，S10，则S1+S2+S3+…+S10= ．
查看答案和解析>>
科目：初中数学 来源： 题型：
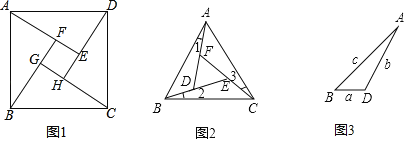
【题目】问题背景：如图1，在正方形ABCD的内部，作∠DAE＝∠ABF＝∠BCG＝∠CDH，根据三角形全等的条件，易得△DAE≌△ABF≌△BCG≌△CDH，从而得四边形EFGH是正方形．
类比探究：如图2，在正△ABC的内部，作∠1＝∠2＝∠3，AD，BE，CF两两相交于D，E，F三点（D，E，F三点不重合）．
（1）△ABD，△BCE，△CAF是否全等？如果是，请选择其中一对进行证明；
（2）△DEF是否为正三角形？请说明理由；
（3）如图3，进一步探究发现，△ABD的三边存在一定的等量关系，设BD＝a，AD＝b，AB＝c，请探索a，b，c满足的等量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
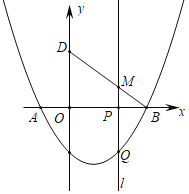
【题目】如图，抛物线y＝
x2+bx+c与x轴交于点A（﹣1，0），B（4，0）与y轴交于点C，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线1，交抛物线与点Q．
（1）求抛物线的解析式；
（2）当点P在线段OB上运动时，直线1交BD于点M，试探究m为何值时，四边形CQMD是平行四边形；
（3）在点P运动的过程中，坐标平面内是否存在点Q，使△BDQ是以BD为直角边的直角三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y＝x2﹣6x+m满足以下条件：当﹣2＜x＜﹣1时，它的图象位于x轴的下方；当8＜x＜9时，它的图象位于x轴的上方，则m的值为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
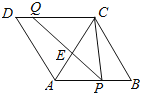
【题目】如图，菱形ABCD的边AB＝8，∠B＝60°，P是AB上一点，BP＝3，Q是CD边上一动点，将梯形APQD沿直线PQ折叠，A的对应点为A′，当CA′的长度最小时，CQ的长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
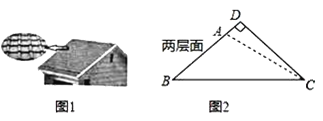
【题目】太阳能光伏建筑是现代绿色环保建筑之一，老张准备把自家屋顶改建成光伏瓦面，改建前屋顶截面△ABC如图2所示，BC=10米，∠ABC=∠ACB=36°，改建后顶点D在BA的延长线上，且∠BDC=90°，求改建后南屋面边沿增加部分AD的长．（结果精确到0.1米）
（参考数据：sin18°≈0.31，cos18°≈0.95．tan18°≈0.32，sin36°≈0.59．cos36°≈0.81，tan36°≈0.73）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在⊿OAB中，∠OAB=90°.OA=AB=6.将⊿OAB绕点O逆时针方向旋转90°得到⊿OA1B1
（1）线段A1B1的长是 ∠AOA1的度数是
（2）连结AA1，求证：四边形OAA1B1是平行四边形 ;
（3）求四边形OAA1B1的面积 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com