
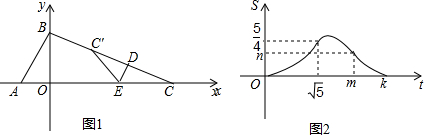
分析 (1)根据直线的解析式先找出点B的坐标,结合图象可知当t=$\sqrt{5}$时,点C′与点B重合,通过三角形的面积公式可求出CE的长度,结合勾股定理可得出OE的长度,由OC=OE+EC可得出OC的长度,即得出C点的坐标,再由勾股定理得出BC的长度,根据CD=$\frac{1}{2}$BC,结合速度=路程÷时间即可得出结论;
(2)结合D点的运动以及面积S关于时间t的函数图象的拐点,即可得知当“当t=k时,点D与点B重合,当t=m时,点E和点O重合”,结合∠C的正余弦值通过解直角三角形即可得出m、k的值,再由三角形的面积公式即可得出n的值;
(3)随着D点的运动,按△DEC′与△BOC的重叠部分形状分三种情况考虑:①通过解直角三角形以及三角形的面积公式即可得出此种情况下S关于t的函数关系式;②由重合部分的面积=S△CDE-S△BC′F,通过解直角三角形得出两个三角形的各边长,结合三角形的面积公式即可得出结论;③通过边与边的关系以及解直角三角形找出BD和DF的值,结合三角形的面积公式即可得出结论.
解答 解:(1)令x=0,则y=2,即点B坐标为(0,2),
∴OB=2.
当t=$\sqrt{5}$时,E和C′点重合,如图1所示,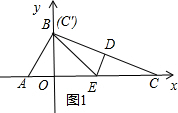
此时S=$\frac{1}{2}$×$\frac{1}{2}$CE•OB=$\frac{5}{4}$,
∴CE=$\frac{5}{2}$,
∴BE=$\frac{5}{2}$.
∵OB=2,
∴OE=$\sqrt{(\frac{5}{2})^{2}-{2}^{2}}$=$\frac{3}{2}$,
∴OC=OE+EC=$\frac{3}{2}$+$\frac{5}{2}$=4,BC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,CD=$\sqrt{5}$,
$\sqrt{5}$÷$\sqrt{5}$=1(单位长度/秒),
∴点D的运动速度为1单位长度/秒,点C坐标为(4,0).
(2)根据图象可知:
当t=k时,点D与点B重合,
此时k=$\frac{BC}{1}$=2$\sqrt{5}$;
当t=m时,点E和点O重合,如图2所示.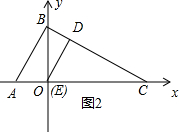
sin∠C=$\frac{OB}{BC}$=$\frac{2}{2\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,cos∠C=$\frac{OC}{BC}$=$\frac{4}{2\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
OD=OC•sin∠C=4×$\frac{\sqrt{5}}{5}$=$\frac{4\sqrt{5}}{5}$,CD=OC•cos∠C=4×$\frac{2\sqrt{5}}{5}$=$\frac{8\sqrt{5}}{5}$.
∴m=$\frac{CD}{1}$=$\frac{8\sqrt{5}}{5}$,n=$\frac{1}{2}$BD•OD=$\frac{1}{2}$×(2$\sqrt{5}$-$\frac{8\sqrt{5}}{5}$)×$\frac{4\sqrt{5}}{5}$=$\frac{4}{5}$.
故答案为:$\frac{8\sqrt{5}}{5}$;$\frac{4}{5}$;2$\sqrt{5}$.
(3)随着D点的运动,按△DEC′与△BOC的重叠部分形状分三种情况考虑:
①当点C′在线段BC上时,如图3所示.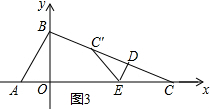
此时CD=t,CC′=2t,0<CC′≤BC,
∴0<t≤$\sqrt{5}$.
∵tan∠C=$\frac{OB}{OC}$=$\frac{1}{2}$,
∴DE=CD•tan∠C=$\frac{1}{2}$t,
此时S=$\frac{1}{2}$CD•DE=$\frac{1}{4}{t}^{2}$;
②当点C′在CB的延长线上,点E在线段OC上时,如图4所示.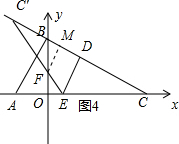
此时CD=t,BC′=2t-2$\sqrt{5}$,DE=CD•tan∠C=$\frac{1}{2}$t,CE=$\frac{CD}{cos∠C}$=$\frac{\sqrt{5}}{2}$t,OE=OC-CE=4-$\frac{\sqrt{5}}{2}$t,
∵$\left\{\begin{array}{l}{CC′>BC}\\{CE≤OC}\end{array}\right.$,即$\left\{\begin{array}{l}{2t>2\sqrt{5}}\\{\frac{\sqrt{5}}{2}t≤4}\end{array}\right.$,
解得:$\sqrt{5}$<t≤$\frac{8\sqrt{5}}{5}$.
由(1)可知tan∠OEF=$\frac{2}{\frac{3}{2}}$=$\frac{4}{3}$,
∴OF=OE•tan∠OEF=$\frac{16}{3}$-$\frac{2\sqrt{5}}{3}$t,BF=OB-OF=$\frac{2\sqrt{5}}{3}$t-$\frac{10}{3}$,
∴FM=BF•cos∠C=$\frac{4}{3}$t-$\frac{4\sqrt{5}}{3}$.
此时S=$\frac{1}{2}$CD•DE-$\frac{1}{2}$BC′•FM=-$\frac{13}{12}{t}^{2}$+$\frac{8\sqrt{5}}{3}$t-$\frac{20}{3}$;
③当点E在x轴负半轴,点D在线段BC上时,如图5所示.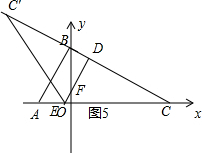
此时CD=t,BD=BC-CD=2$\sqrt{5}$-t,CE=$\frac{\sqrt{5}}{2}$t,DF=$\frac{BD}{tan∠C}$=2BD=4$\sqrt{5}$-2t,
∵$\left\{\begin{array}{l}{CE>OC}\\{CD≤BC}\end{array}\right.$,即$\left\{\begin{array}{l}{\frac{\sqrt{5}}{2}t>4}\\{t≤2\sqrt{5}}\end{array}\right.$,
∴$\frac{8\sqrt{5}}{5}$<t≤2$\sqrt{5}$.
此时S=$\frac{1}{2}$BD•DF=$\frac{1}{2}$×2×$(2\sqrt{5}-t)^{2}$=t2-4$\sqrt{5}$t+20.
点评 本题考查了勾股定理、解直角三角形以及三角形的面积公式,解题的关键是:(1)求出BC、OC的长度;(2)根据图象能够了解当t=m和t=k时,点DE的位置;(3)分三种情况求出S关于t的函数关系式.本题属于中档题,(1)(2)难度不大;(3)需要画出图形,利用数形结合,通过解直角三角形以及三角形的面积公式找出S关于t的函数解析式.


科目:初中数学 来源: 题型:填空题
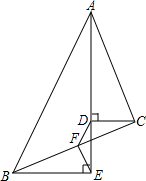 如图,△ABC中,AE平分∠BAC,CD⊥AE于D,BE⊥AE,F为BC中点,连结DF、EF,若AB=10,AC=6,∠DFE=135°,则△DEF的面积是$\sqrt{2}$.
如图,△ABC中,AE平分∠BAC,CD⊥AE于D,BE⊥AE,F为BC中点,连结DF、EF,若AB=10,AC=6,∠DFE=135°,则△DEF的面积是$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
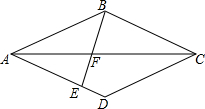 如图,菱形ABCD,过点B作直线BE,使得∠ABE=∠BCA,分别交AC、AD于点F、E.若AB=CF.则$\frac{AE}{AD}$=$\frac{\sqrt{5}-1}{2}$.
如图,菱形ABCD,过点B作直线BE,使得∠ABE=∠BCA,分别交AC、AD于点F、E.若AB=CF.则$\frac{AE}{AD}$=$\frac{\sqrt{5}-1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
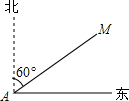 如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里,那么该船继续航行多少海里可使渔船到达离灯塔距离最近的位置( )
如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里,那么该船继续航行多少海里可使渔船到达离灯塔距离最近的位置( )| A. | 50$\sqrt{3}$ | B. | 40 | C. | 30 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com