
【题目】某学校办公楼前有一长为![]() ,宽为
,宽为![]() 的长方形空地,在中心位置留出一个直径为
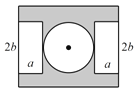
的长方形空地,在中心位置留出一个直径为![]() 的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.
的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.
(1)用含字母和![]() 的式子表示阴影部分的面积;
的式子表示阴影部分的面积;
(2)当![]() =8,
=8,![]() =6,
=6,![]() =1,
=1,![]() =2时,阴影部分的面积是多少?(
=2时,阴影部分的面积是多少?(![]() 取 3.)
取 3.)
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④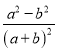 . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);
(2)若![]() 为正整数,且
为正整数,且![]() 为“和谐分式”,请写出
为“和谐分式”,请写出![]() 的值;
的值;
(3)在化简![]() 时,
时,
小东和小强分别进行了如下三步变形:
小东: ![]()
![]()

小强: ![]()
![]()
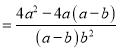
显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】孝感市在创建国家级园林城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )
A.3,3,0.4
B.2,3,2
C.3,2,0.4
D.3,3,2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上,点 A 的初始位置表示的数为 1,现点 A 做如下移动:第 1 次点 A 向左移动 3 个单位长度至点 A1,第 2 次从点 A1 向右移动 6 个单位长度至点 A2,第 3 次从点 A2 向左移动 9 个单位长度至点 A3,…,按照这种移动方式进行下去,点 A4 表示的数,是__________ ,如果点 An 与原点的距离不小于 20, 那么 n 的最小值是________________ .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+b与反比例函数y= ![]() (x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点.
(x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点. 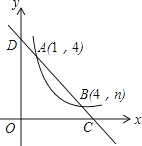
(1)m= , n=;若M(x1 , y1),N(x2 , y2)是反比例函数图象上两点,且0<x1<x2 , 则y1y2(填“<”或“=”或“>”);
(2)若线段CD上的点P到x轴、y轴的距离相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,但是由于
的小数部分我们不可能全部地写出来,但是由于![]() ,所以
,所以![]() 的整数部分为1,将
的整数部分为1,将![]() 减去其整数部分1,所得的差就是其小数部分
减去其整数部分1,所得的差就是其小数部分![]() ,根据以上的内容,解答下面的问题:
,根据以上的内容,解答下面的问题:
![]() 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______;
![]() 的整数部分是______,小数部分是______;
的整数部分是______,小数部分是______;
![]() 整数部分是______,小数部分是______;
整数部分是______,小数部分是______;
![]() 若设
若设![]() 整数部分是x,小数部分是y,求
整数部分是x,小数部分是y,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八个边长为1的正方形如图所示的位置摆放在平面直角坐标系中,经过原点的直线l将这八个正方形分成面积相等的两部分,则这条直线的解析式是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com