
【题目】八个边长为1的正方形如图所示的位置摆放在平面直角坐标系中,经过原点的直线l将这八个正方形分成面积相等的两部分,则这条直线的解析式是_____.

【答案】y=![]() x
x
【解析】
设直线l和八个正方形的最上面交点为A,过点A作AB⊥y轴于点B,过点A作AC⊥x轴于点C,易知OB=3,利用三角形的面积公式和已知条件求出A的坐标,再利用待定系数法可求出该直线l的解析式.
设直线l和八个正方形的最上面交点为A,过点A作AB⊥y轴于点B,过点A作AC⊥x轴于点C,如图所示.
∵正方形的边长为1,∴OB=3.
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,∴两部分面积分别是4,∴三角形ABO面积是5,∴![]() OBAB=5,∴AB=
OBAB=5,∴AB=![]() ,∴OC=
,∴OC=![]() ,∴点A的坐标为(
,∴点A的坐标为(![]() ,3).
,3).
设直线l的解析式为y=kx,
∵点A(![]() ,3)在直线l上,∴3=
,3)在直线l上,∴3=![]() k,
k,
解得:k=![]() ,∴直线l解析式为y=
,∴直线l解析式为y=![]() x.
x.
故答案为:y=![]() x.
x.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
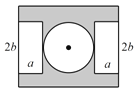
【题目】某学校办公楼前有一长为![]() ,宽为
,宽为![]() 的长方形空地,在中心位置留出一个直径为
的长方形空地,在中心位置留出一个直径为![]() 的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.
的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.
(1)用含字母和![]() 的式子表示阴影部分的面积;
的式子表示阴影部分的面积;
(2)当![]() =8,
=8,![]() =6,
=6,![]() =1,
=1,![]() =2时,阴影部分的面积是多少?(
=2时,阴影部分的面积是多少?(![]() 取 3.)
取 3.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( ) 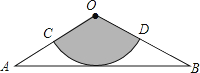
A.10cm
B.15cm
C.10 ![]() cm
cm
D.20 ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某运算程序,该程序是循环迭代的一种.根据该程序的指令,如果输入![]() 的值是10,那么得到第1次输出的值是5;把第1次输出的值再次输入,那么第2次输出的值是6;把第2次输出的值再次输入,那么第3次输出的值是3;…,第2018次输出的值是( )
的值是10,那么得到第1次输出的值是5;把第1次输出的值再次输入,那么第2次输出的值是6;把第2次输出的值再次输入,那么第3次输出的值是3;…,第2018次输出的值是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动.已知点A的速度是1单位长度/秒,点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
(1)求请在数轴上标出A、B两点从原点出发运动3秒时的位置;
![]()
(2)若A、B两点在(1)中的位置,数轴上是否存在一点P到点A,点B的距离之和为16,并求出此时点P表示的数;若不存在,请说明理由.
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以10单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列图形都是由相同的正方形按一定的规律组成,其中:第(1)个图形中的正方形有2个,第(2)个图形中的正方形有5个,第(3)个图形中的正方形有9个,…,按此规律,则第7个图形中的正方形的个数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发商进行商铺促销,广告上写着如下条款:
购买商铺后,都由开发商代为租赁10年,10年期满后再由开发商以比原商铺标价高20%的价格进行回购,投资者可在以下两种购铺方案中做出选择:
方案一:投资者按商铺标价一次性付清铺款,每年可以获得的租金为商铺标价的5%.
方案二:投资者按商铺标价的八五折一次性付清铺款,4年后每年可以获得的租金为商铺标价的5%,但要缴纳租金的10%作为管理费用.
(1)请问:投资者选择哪种购铺方案,10年后所获得的投资收益率更高?为什么?(注:投资收益率=![]() ×100%)
×100%)
(2)(列方程求解)某投资者按方案一购买商铺,因资金周转,决定向银行贷铺款的20%并于一年后付清贷款,已知贷款年利率为5%.那么10年后该投资者获得55.2万元的收益,问铺款是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:
千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:

回答下列问题:
(1)这![]() 筐白菜中,最接近
筐白菜中,最接近![]() 千克的那筐白菜为 千克;
千克的那筐白菜为 千克;
(2)若白菜每千克售价![]() 元,则出售这8筐白菜可卖多少元?
元,则出售这8筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com