
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
科目:初中数学 来源: 题型:
【题目】如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( ) 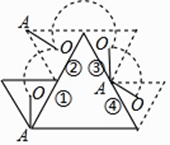
A.240°
B.360°
C.480°
D.540°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商场电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商场用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商场准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13200元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,某住宅小区在施工过程中留下了一块空地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,点A在x轴的正半轴上,点B、C在第一象限,且四边形OABC是平行四边形,OC=2 ![]() ,sin∠AOC=
,sin∠AOC= ![]() ,反比例函数y=
,反比例函数y= ![]() 的图象经过点C以及边AB的中点D.
的图象经过点C以及边AB的中点D. 
(1)求这个反比例函数的解析式;
(2)四边形OABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
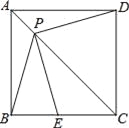
【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,我们把横、纵坐标都为整数的点称为整点,记定点都是整点的三角形为整点三角形.如图,已知整点O(0,0),A(2,4),请在所给网格区域(含边界)上按要求画图.
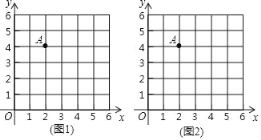
(1)在图1中画一个整点三角形OAB,其中点B在第一象限,且点B的横、纵坐标之和等于点A的横坐标;
(2)在图2中画一个整点三角形OAC,其中点C的坐标为(3t,t),且点C的横、纵坐标之和是点A的纵坐标的2倍.请直接写出△OAC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC. 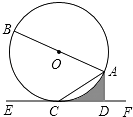
(1)求证:EF是⊙O的切线;
(2)求证:AC2=ADAB;
(3)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com