
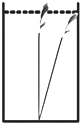
 在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”这个数学问题的意思是说:“有一个水池,水面是一个边长为1丈(1丈=10尺)的正方形,在水池正中央长有一根芦苇,芦苇露出水面 1 尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各是多少?”设这个水池的深度是x尺,根据题意,可列方程为x2+52=(x+1)2.
在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何?”这个数学问题的意思是说:“有一个水池,水面是一个边长为1丈(1丈=10尺)的正方形,在水池正中央长有一根芦苇,芦苇露出水面 1 尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各是多少?”设这个水池的深度是x尺,根据题意,可列方程为x2+52=(x+1)2.  挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
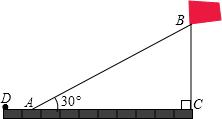 如图,小明利用升旗用的绳子测量学校旗杆BC的高度,当绳子从旗杆端垂下,地上部分还有8米,若把绳子往外拉直,绳子末端接触地面A点并与地面形成30°角,求旗杆BC的高度.
如图,小明利用升旗用的绳子测量学校旗杆BC的高度,当绳子从旗杆端垂下,地上部分还有8米,若把绳子往外拉直,绳子末端接触地面A点并与地面形成30°角,求旗杆BC的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
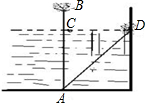 水池中离岸边D点1.5米的C处,直立长着一根芦苇,出水部分BC的长是0.5米,把芦苇拉到岸边,它的顶端B恰好落到D点,并求水池的深度AC.
水池中离岸边D点1.5米的C处,直立长着一根芦苇,出水部分BC的长是0.5米,把芦苇拉到岸边,它的顶端B恰好落到D点,并求水池的深度AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9,12,14 | B. | 2,$\sqrt{2}$,$\sqrt{3}$ | C. | 4,3,$\sqrt{5}$ | D. | 4,3,5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
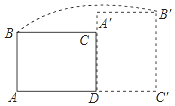 如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是多少?(结果保留π).
如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是多少?(结果保留π).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com