
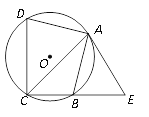
【题目】如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
(1)求证:AE是⊙O的切线;
(2)若AB=AD,AC=![]() ,tan∠ADC=3,求BE的长.
,tan∠ADC=3,求BE的长.
【答案】(1)证明见解析;(2)![]()
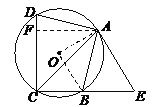
【解析】试题分析:(1)连接OA、OB,由圆周角定理得出∠AOB=2∠ACB=90°,由等腰直角三角形的性质得出∠OAB=∠OBA=45°,求出∠OAE=∠OAB+∠BAE=90°,即可得出结论;(2)过点A作AF⊥CD于点F,由AB=AD,得到∠ACD=∠ACB=45°,在Rt△AFC中可求得AF=3,在Rt△AFD中求得DF=1,所以AB=![]() =
=![]() ,CD= CF+DF=4,再证明△ABE∽△CDA,得出
,CD= CF+DF=4,再证明△ABE∽△CDA,得出![]() ,即可求出BE的长度;
,即可求出BE的长度;
试题解析:
(1)证明:连结OA,OB,
∵∠ACB=45°,
∴∠AOB=2∠ACB= 90°,
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BAE=45°,
∴∠OAE=∠OAB+∠BAE=90°,
∴OA⊥AE.
∵点A在⊙O上,
∴AE是⊙O的切线.
(2)解:过点A作AF⊥CD于点F,则∠AFC=∠AFD=90°.
∵AB=AD,
∴![]() =
=![]()
∴∠ACD=∠ACB=45°,
在Rt△AFC中,
∵AC=![]() ,∠ACF=45°,
,∠ACF=45°,
∴AF=CF=AC·sin∠ACF =3,
∵在Rt△AFD中, tan∠ADC=![]() ,
,
∴DF=1,
∴![]() ,
,
且CD= CF+DF=4,
∵四边形ABCD内接于⊙O,
∴∠ABE=∠CDA,
∵∠BAE=∠DCA,
∴△ABE∽△CDA,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】小河两岸边各有一棵树,分别高30尺和20尺,两树的距离是50尺,每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见水面上游出一条鱼,它们立刻飞去抓鱼,速度相同,并且同时到达目标.则这条鱼出现的地方离开比较高的树的距离为尺.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A. ab+ac+ad+1=a(b+c+d)+1
B. (x+1)(x+2)=x2+3x+2
C. a3+3a2b+a=a(a2+3ab+1)
D. x2-y2=(x+y)(y-x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,举行抽奖活动,并规定:顾客每购买100元的商品,就可随机抽取一张奖券,抽得奖券“紫气东来”、“花开富贵”、“吉星高照”,就可以分别获得100元、50元、20元的购物券,抽得“谢谢惠顾”不赠购物券;如果顾客不愿意抽奖,可以直接获得购物券10元。小明购买了100元的商品,他看到商场公布的前10000张奖券的抽奖结果如下:
奖券种类 | 紫气东来 | 花开富贵 | 吉星高照 | 谢谢惠顾 |
出现张数(张) | 500 | 1000 | 2000 | 6500 |
(1)求“紫气东来”奖券出现的频率;
(2)请你帮助小明判断,抽奖和直接获得购物卷,哪种方式更合算?并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,线段AB的端点坐标为A(-2,4),B(4,2),直线y=kx-2与线段AB有交点,则k的值不可能是( )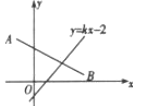
A.-5
B.-2
C.3
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com