解:(1)抛物线的对称轴是直线x=-

=

,
解得b=-3,
∵点B(3,0)在抛物线上,
∴9-3×3+c=0,
解得c=0.
所以此抛物线的表达式为y=x
2-3x;
(2)存在.
理由如下:令y=0,则x
2-3x=0,

解得x
1=0,x
2=3,
∵点A在点B左边,
∴点A的坐标为(0,0),
∴AB=3,
设点M到AB的距离为h,则S
△AMB=

×3•h=3,
解得h=2,
∵△AMB是锐角三角形,
∴点M应该在x轴的下方,
∴点M的纵坐标为-2,
代入抛物线解析式得,x
2-3x=-2,
即x
2-3x+2=0,
解得x
1=1,x
2=2,
又∵点M在对称轴右边的图象上,
∴点M的横坐标为2,
∴点M的坐标为(2,-2),
此时,过点M作MN⊥x轴于点N,则AN=MN=2,BN=1,
∴∠AMN=45°,∠BMN<45°,

∴∠AMB<90°,是锐角,
∴△AMB是锐角三角形,
故存在点M(2,-2),使锐角三角形AMB的面积等于3;
(3)由(2)得∠MAN=45°,
∵∠PAM=90°,
∴∠PAN=90°-45°=45°,
∴点P在直线y=x上,
联立

,
解得
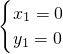
(舍去),
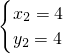
,
∴点P的坐标为(4,4),
根据勾股定理,AM=
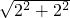
=2

,
PA=

=4

,
所以△APM的面积=

AM•PM=

×2

×4

=8.
分析:(1)根据抛物线对称轴解析式列式求出b,再把点B的坐标代入求出c,即可得解;
(2)根据抛物线解析式求出点A的坐标,再求出AB的长度,然后利用三角形的面积公式求出点M到AB的距离,然后根据△AMB是锐角三角形判断点M在x轴下方,从而确定点M的纵坐标,再代入抛物线解析式计算求出横坐标,从而得解;
(3)根据点M的坐标可得∠BAM=45°,然后求出∠PAB=45°,从而写出直线PA的解析式,与抛物线解析式联立求出点P的坐标,再利用勾股定理求出PA、AM的长度,然后根据直角三角形的面积等于两直角边乘积的一半计算即可得解.
点评:本题是对二次函数的综合考查,主要利用了二次函数的对称轴,点在抛物线上,三角形的面积,直角三角形的面积以及直线与抛物线的交点的求解,难度不是很大,先求出抛物线的解析式是解题的关键,数据的巧妙设计也是本题的一大特点.

 .
. =
= ,
,
 ×3•h=3,
×3•h=3,
 ,
,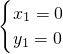 (舍去),
(舍去),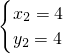 ,
,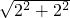 =2
=2 ,
, =4
=4 ,
, AM•PM=
AM•PM= ×2
×2 ×4
×4 =8.
=8.

 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案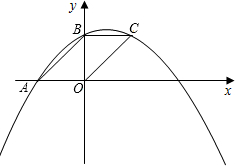 (1)求b+c的值;
(1)求b+c的值;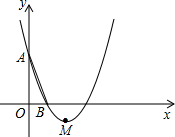 (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.