
分析 根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2015除以4,根据商和余数的情况确定点A2015的坐标即可.
解答 解:∵点A1的坐标为(3,1),
∴A2(-1+1,3+1)即(0,4),A3(-3,-1+2)即(-3,1),A4(1-1,-3+1)即(0,-2),A5(3,1),
…,
依此类推,每4个点为一个循环组依次循环,
∵2015÷4=503余3,
∴点A2015的坐标与A3的坐标相同,为(-3,-1+2),即(-3,1);
故答案为:(0,-2);(-3,1).
点评 此题考查点的坐标规律,读懂题目信息,理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:选择题
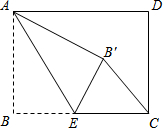 矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )| A. | 3 | B. | $\frac{3}{2}$ | C. | 2或3 | D. | 3或$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
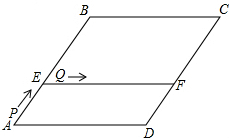 如图,在菱形ABCD中,AB=10,sinA=$\frac{4}{5}$,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.
如图,在菱形ABCD中,AB=10,sinA=$\frac{4}{5}$,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
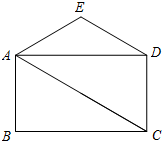 如图,四边形ABCD为矩形,DE∥AC,且DE=AB,过点E作AD的垂线交AC于点F.
如图,四边形ABCD为矩形,DE∥AC,且DE=AB,过点E作AD的垂线交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
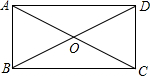 如图所示,在矩形ABCD中,DG⊥AC,G为垂足,∠CDG:∠GDA=1:3,那么∠BDG=45°,若AC=8,那么DG=2$\sqrt{2}$.
如图所示,在矩形ABCD中,DG⊥AC,G为垂足,∠CDG:∠GDA=1:3,那么∠BDG=45°,若AC=8,那么DG=2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
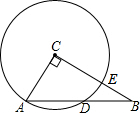 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )| A. | $\frac{18}{5}$ | B. | $\frac{5}{2}$ | C. | $\frac{24}{5}$ | D. | $\frac{9}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,CO⊥AB于O,D在⊙O上,连接BD,CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.
如图,AB为⊙O的直径,CO⊥AB于O,D在⊙O上,连接BD,CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com