
 如图,正方形ABCD的边长为2cm,以边BC为直径作半圆O,点E在AB上,且AE=1.5cm,连接DE.
如图,正方形ABCD的边长为2cm,以边BC为直径作半圆O,点E在AB上,且AE=1.5cm,连接DE.分析 (1)过点O作OF⊥DE,垂足为点F,在Rt△ADE中利用勾股定理计算出DE=2.5,再利用面积法求出OF=1,然后根据切线的判定方法可判断DE与半圆O相切;
(2)利用阴影部分的面积=梯形BECD的面积-半圆的面积求解.
解答 解:(1)DE与半圆O相切.理由如下:
过点O作OF⊥DE,垂足为点F,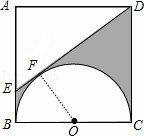
在Rt△ADE中,∵AD=2,AE=1.5,
∴DE=$\sqrt{{2}^{2}+1.{5}^{2}}$=2.5,
∵S四边形BCDE=S△DOE+S△BOE+S△CDO,
∴$\frac{1}{2}$(0.5+2)×2=$\frac{1}{2}$×2.5•OF+$\frac{1}{2}$×1×0.5+$\frac{1}{2}$×1×2,
∴OF=1,
∵OF的长等于圆O的半径,OF⊥DE,
∴DE与半圆O相切;
(2)阴影部分的面积=梯形BECD的面积-半圆的面积
=$\frac{1}{2}$×(0.5+2)×2-$\frac{1}{2}$•π•12
=$\frac{5-π}{2}$(cm2).
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.注意把不规律图形的面积的计算问题化为规则图形面积的和差的计算问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
 如图,一次函数y=-2x+4的图象与x轴、y轴分别交于点A、B、O为坐标原点,OA,AB的中点分别为点C,D,点P为OB上一动点,当PC+PD的值最小时,点P的坐标为(0,1).
如图,一次函数y=-2x+4的图象与x轴、y轴分别交于点A、B、O为坐标原点,OA,AB的中点分别为点C,D,点P为OB上一动点,当PC+PD的值最小时,点P的坐标为(0,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 李大爷按每千克2.1元批发了一批黄瓜到镇上出售,为了方便,他带了一些零钱备用.他先按市场售出一些后,又降低出售.售出黄瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
李大爷按每千克2.1元批发了一批黄瓜到镇上出售,为了方便,他带了一些零钱备用.他先按市场售出一些后,又降低出售.售出黄瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为y米,乙行驶的时间为x秒,y与x之间的关系如图所示.若丙也从甲出发的地方沿相同的方向骑自行车行驶,且与甲的速度相同,当甲追上乙后45秒时,丙也追上乙,则丙比甲晚出发15秒.
甲、乙两人骑自行车匀速同向行驶,乙在甲前面100米处,同时出发去距离甲1300米的目的地,其中甲的速度比乙的速度快.设甲、乙之间的距离为y米,乙行驶的时间为x秒,y与x之间的关系如图所示.若丙也从甲出发的地方沿相同的方向骑自行车行驶,且与甲的速度相同,当甲追上乙后45秒时,丙也追上乙,则丙比甲晚出发15秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com