
【题目】如图1,点P是菱形ABCD的对角线BD上的一动点,连接CP并延长交AD于E,交BA的延长线于点F.
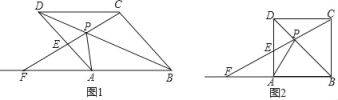
(1)求证:△APD≌△CPD;
(2)如图2,当菱形ABCD变为正方形,且PC=2,tan∠PFA=![]() 时,求正方形ABCD的边长.
时,求正方形ABCD的边长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据菱形的性质得:AD=CD,∠ADP=∠CDP,根据SAS即可证明△APD≌△CPD;
(2)先根据tan∠PFA![]() ,设BC=a,则BF=2a,证明△DPC∽△BPF,得
,设BC=a,则BF=2a,证明△DPC∽△BPF,得![]() ,求FC=6,根据勾股定理列方程得:62=a2+(2a)2,可得正方形ABCD的边长.
,求FC=6,根据勾股定理列方程得:62=a2+(2a)2,可得正方形ABCD的边长.
(1)∵四边形ABCD是菱形,∴AD=CD,∠ADP=∠CDP.
在△APD和△CPD中,∵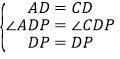 ,∴△APD≌△CPD(SAS);
,∴△APD≌△CPD(SAS);
(2)∵四边形ABCD是正方形,∴∠ABC=90°,CD=BC.
∵tan∠PFA![]() ,设BC=a,则BF=2a.
,设BC=a,则BF=2a.
∵DC=BC=a,DC∥BF,∴∠DCP=∠PFB,∠CDP=∠PBF,∴△DPC∽△BPF,∴![]() .
.
∵PC=2,∴PF=4,∴FC=PC+PF=6.
在Rt△FCB中,FC2=BC2+FB2,∴62=a2+(2a)2,解得:a![]() 或
或![]() (舍),∴正方形ABCD的边长为
(舍),∴正方形ABCD的边长为![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
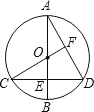
【题目】如图,已知⊙O 的直径 AB 垂直弦 CD 于点 E,连接 CO 并延长交 AD于点 F,且 CF⊥AD
(1)求证:点 E 是 OB 的中点;
(2)若 AB=12,求 CD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的长
的长
(2)若点![]() 是射线
是射线![]() 上的一个动点,作
上的一个动点,作![]() 于点
于点![]() ,连结
,连结![]() .
.
①当点![]() 在线段
在线段![]() 上时,若
上时,若![]() 是以
是以![]() 为腰的等腰三角形,请求出所有符合条件的
为腰的等腰三角形,请求出所有符合条件的![]() 的长.
的长.
②设![]() 交直线
交直线![]() 于点
于点![]() ,连结
,连结![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的长为______________.(直接写出结果)
的长为______________.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() 是边
是边![]() 上一点,连接
上一点,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,则有以下四个结论:①
,则有以下四个结论:①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() 的周长是10;④
的周长是10;④![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
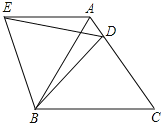
A.②③④B.①③④C.①②④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
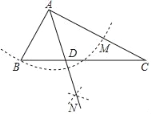
【题目】如图,Rt△ABC中,∠BAC=90°,AB=6,sinC=![]() ,以点A为圆心,AB长为半径作弧交AC于M,分别以B、M为圆心,以大于
,以点A为圆心,AB长为半径作弧交AC于M,分别以B、M为圆心,以大于![]() BM长为半径作弧,两弧相交于点N,射线AN与BC相交于D,则AD的长为_____.
BM长为半径作弧,两弧相交于点N,射线AN与BC相交于D,则AD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图(1)、(2)所示的△ABC中,AB=4,AC=6.将△ABC沿图示中的虚线剪开裁剪办法已在图上标注,对于各图中剪下的两个阴影三角形而言,下列说法正确的是( )
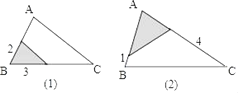
A. 只有(1)中的与△ABC相似 B. 只有(2)中的与△ABC相似
C. 都与△ABC相似 D. 都与△ABC不相似
查看答案和解析>>
科目:初中数学 来源: 题型:
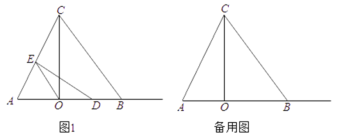
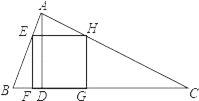
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E,H分别在AB,AC上,已知BC=40cm,AD=30cm,求这个正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由8个大小相同的小正方体组合成的简单几何体.
(1)该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图;(边框线加粗画出,并涂上阴影)
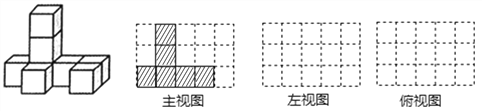
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和主视图不变,那么请在下列网格图中画出添加小正方体后所得几何体所有可能的左视图.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com