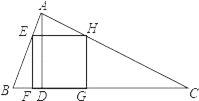
【题目】如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E，H分别在AB，AC上，已知BC=40cm，AD=30cm，求这个正方形的边长．
科学实验活动册系列答案科目：初中数学 来源： 题型：
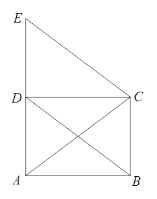
【题目】已知：如图，四边形ABCD是平行四边形，CE∥BD交AD的延长线于点E，CE=AC．
（1）求证：四边形ABCD是矩形；
（2）若AB=4，AD=3，求四边形BCED的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，点M的坐标为（x1，y1），点N的坐标为（x2，y2），且x1≠x2，y1≠y2，以MN为边构造菱形，若该菱形的两条对角线分别平行于x轴，y轴，则称该菱形为边的“坐标菱形”．
（1）已知点A（1，0），B（0，
），则以AB为边的“坐标菱形”的最小内角为______；
（2）若点C（2，1），点D在直线y=5上，以CD为边的坐标菱形”为正方形，求育直线CD表达式；
（3）⊙O的半径为
，点P的坐标为（3，m），若在⊙O上存在一点Q，使得以QP为边的“坐标菱形”为正方形，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，点P是菱形ABCD的对角线BD上的一动点，连接CP并延长交AD于E，交BA的延长线于点F．
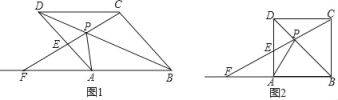
（1）求证：△APD≌△CPD；
（2）如图2，当菱形ABCD变为正方形，且PC=2，tan∠PFA=
时，求正方形ABCD的边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知
，
.点
在
上以
的速度由点
向点
运动，同时点
在
上由点向点
运动，它们运动的时间为
．
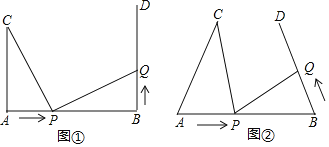
（1）如图①，
，
，若点的运动速度与点的运动速度相等，当
时，
与
是否全等，请说明理由，并判断此时线段
和线段
的位置关系；
（2）如图②，将图①中的“，”为改“
”，其他条件不变．设点的运动速度为
，是否存在实数
，使得与全等？若存在，求出相应的、
的值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于任意三个实数a，b，c，用min|a，b，c|表示这三个实数中最小数，例如：min|-2，0，1|=-2，则：
（1）填空，min|（-2019）0，（-
）-2，-
|=______，如果min|3，5-x，3x+6|=3，则x的取值范围为______；
（2）化简：
÷（x+2+
）并在（1）中x的取值范围内选取一个合适的整数代入求值．
查看答案和解析>>
科目：初中数学 来源： 题型：
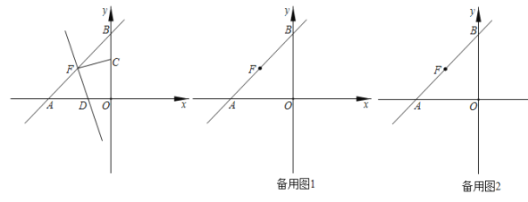
【题目】如图，已知直线
经过点
，交x轴于点A，y轴于点B，F为线段AB的中点，动点C从原点出发，以每秒1个位长度的速度沿y轴正方向运动，连接FC，过点F作直线FC的垂线交x轴于点D，设点C的运动时间为t秒．
当
时，求证：
；
连接CD，若
的面积为S，求出S与t的函数关系式；
在运动过程中，直线CF交x轴的负半轴于点G，
是否为定值？若是，请求出这个定值；若不是，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
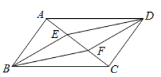
【题目】如图，在□ABCD中，E，F是对角线AC上的两点且AE＝CF，在①BE＝DF；②AB＝DE；③BE∥DF；④四边形EBFD为菱形；⑤S△ADE＝S△ABE；⑥AF＝CE，这些结论中正确的是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
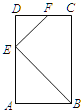
【题目】如图，在矩形ABCD中，AB=6，AD=12，点E在AD边上，且AE=8，EF⊥BE交CD于点F.
（1）求证：△ABE∽△DEF；
（2）求CF的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
