
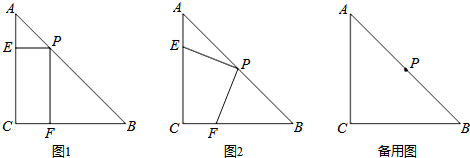
���� ��1����ͼ1����֤��AEP�ס�PFB��Ȼ���������������ε����ʼ��ɽ�����⣻
��2������CP����ͼ2����֤��APE�ա�CPF���Ӷ��õ�PE=PF���ʣ�1���Ľ��۲�������
��3���ڣ�2���������¿ɵ�AE=CF���ɴ˿ɵ�EC+CF=2��EF=$\frac{2}{3}$$\sqrt{6}$����CF=x����Rt��CEF�����ù��ɶ��������CF��ֵ������CF��ֵ�������������������������ۣ�����CF=$\frac{3-\sqrt{3}}{3}$����ͼ3������P��PH��BC��H�������PH��FH��Ȼ����Rt��PHF���������Ǻ����������FPH�Ķ������ɴ˿��������ֵ������CF=$\frac{3+\sqrt{3}}{3}$����ͼ4������P��PG��AC��G��ͬ���������APE�������ɴ˿��������ֵ��
��� �⣺��1����ͼ1��
��PE��AC��
���AEP=��PEC=90�㣮
�֡ߡ�EPF=��ACB=90�㣬
���ı���PECFΪ���Σ�
���PFC=90�㣬
���PFB=90�㣬
���AEP=��PFB��
��AC=BC����C=90�㣬
���A=��B=45�㣬
���FPB=��B=45�㣬��AEP�ס�PFB��
��PF=BF��$\frac{PE}{BF}$=$\frac{AP}{PB}$��
��$\frac{PE}{PF}$=$\frac{AP}{PB}$=$\frac{1}{3}$��
��2����1���Ľ��۲��������������£�
����PC����ͼ2��
��$\frac{AP}{PB}$=1��
���P��AB���е㣮
�֡ߡ�ACB=90�㣬CA=CB��
��CP=AP=$\frac{1}{2}$AB����ACP=��BCP=$\frac{1}{2}$��ACB=45�㣬CP��AB��
���APE+��CPE=90�㣮
�ߡ�CPF+��CPE=90�㣬
���APE=��CPF��
�ڡ�APE�͡�CPF�У�
$\left\{\begin{array}{l}{��A=��PCF=45��}\\{PA=PC}\\{��APE=��CPF}\end{array}\right.$��
���APE�ա�CPF��
��AE=CF��PE=PF��
�ʣ�1���еĽ���$\frac{PE}{PF}$=$\frac{1}{3}$��������
��3������CEF���ܳ�����2+$\frac{2}{3}$$\sqrt{6}$ʱ�����Ķ���Ϊ75���15�㣮
��ʾ���ڣ�2���������£��ɵ�AE=CF����֤����
��EC+CF=EC+AE=AC=2��
��EC+CF+EF=2+$\frac{2}{3}$$\sqrt{6}$��
��EF=$\frac{2}{3}$$\sqrt{6}$��
��CF=x������CE=2-x��
��Rt��CEF�У����ݹ��ɶ����ɵ�x2+��2-x��2=��$\frac{2}{3}$$\sqrt{6}$��2��
�����ã�3x2-6x+2=0��
��ã�x1=$\frac{3-\sqrt{3}}{3}$��x2=$\frac{3+\sqrt{3}}{3}$��
����CF=$\frac{3-\sqrt{3}}{3}$����ͼ3��
����P��PH��BC��H��
��PH=HB=CH=1��FH=1-$\frac{3-\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$��
��Rt��PHF��tan��FPH=$\frac{FH}{PH}$=$\frac{\sqrt{3}}{3}$��
���FPH=30�㣬
���=��FPB=30+45��=75�㣻
����CF=$\frac{3+\sqrt{3}}{3}$����ͼ4��
����P��PG��AC��G��
ͬ���ɵã���APE=75�㣬
���=��FPB=180��-��APE-��EPF=15�㣮
���� ������Ҫ���������������ε��ж������ʡ�ȫ�������ε��ж������ʡ����ε��ж������ʡ����������ε����ʡ�ֱ��������б���ϵ����ߵ���б�ߵ�һ�롢���Ǻ����Ķ��塢����ǵ����Ǻ���ֵ�����ɶ�����֪ʶ����һ�����ۺ��ԣ��õ�EC+CF=2�ǽ���ڣ�3��С��Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
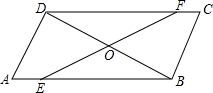 ��ͼ��?ABCD�У���E��F�ֱ���AB��CD�ϣ���AE=CF��EF��BD�ཻ�ڵ�O����֤��OB=OD��
��ͼ��?ABCD�У���E��F�ֱ���AB��CD�ϣ���AE=CF��EF��BD�ཻ�ڵ�O����֤��OB=OD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
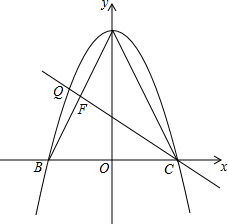 ��ͼ���ڡ�ABC�У�AB=AC����A��0��4����B��-2��0����C��2��0����F��AB���е㣬��AΪ����������߾���B��C��������ֱ��CF���ڵ�Q��
��ͼ���ڡ�ABC�У�AB=AC����A��0��4����B��-2��0����C��2��0����F��AB���е㣬��AΪ����������߾���B��C��������ֱ��CF���ڵ�Q���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{{\begin{array}{l}{a=4}\\{b=1}\end{array}}\right.$ | B�� | $\left\{{\begin{array}{l}{a=-4}\\{b=-1}\end{array}}\right.$ | C�� | $\left\{{\begin{array}{l}{a=-4}\\{b=1}\end{array}}\right.$ | D�� | $\left\{{\begin{array}{l}{a=4}\\{b=-1}\end{array}}\right.$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com