
【题目】如图,在四边形![]() 中,
中,![]() 的角平分线与边
的角平分线与边![]() 交于点
交于点![]() ,
,![]() 的角平分线交直线
的角平分线交直线![]() 于点
于点![]() .
.
(1)若点![]() 在四边形
在四边形![]() 的内部,
的内部,
①如图,若![]() ,
,![]() ,
,![]() ,则
,则![]() _______°;
_______°;
②如图,试探索![]() 、
、![]() 、
、![]() 之间的数量关系,并将你的探索过程写下来.
之间的数量关系,并将你的探索过程写下来.
(2)如图,若点![]() 是四边形
是四边形![]() 的外部,请你直接写出
的外部,请你直接写出![]() 、
、![]() 、
、![]() 之间的数量关系.
之间的数量关系.

【答案】(1)①![]() ;②
;②![]()
![]() ;(2)
;(2)![]() .
.
【解析】
(1)①根据平行线的性质和角平分线的定义可求∠BAE,∠CDO,再根据三角形外角的性质可求∠AEC,再根据四边形内角和等于360°可求∠DOE的度数;
②根据三角形外角的性质和角平分线的定义可得∠DOE和∠BAD、∠ADC的关系,再根据四边形内角和等于360°可求∠B、∠C、∠DOE之间的数量关系;
(2)根据四边形和三角形的内角和得到∠BAD+∠ADC=360°-∠B-∠C,∠EAD+∠ADO=180°-∠DOE,根据角平分线的定义得到∠BAD=2∠EAD,∠ADC=2∠ADO,于是得到结论.
解:(1)①)①∵AD∥BC,∠B=40°,∠C=70°,
∴∠BAD=140°,∠ADC=110°,
∵AE、DO分别平分∠BAD、∠CDA,
∴∠BAE=70°,∠ODC=55°,
∴∠AEC=110°,
∴∠DOE=360°-110°-70°-55°=125°;
故答案为:125;
②![]() 平分
平分![]()
![]()
![]() 平分
平分![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
(2)![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场欲购进一种商品,当购进这种商品至少为10kg,但不超过30kg时,成本y(元/kg)与进货量x(kg)的函数关系如图所示.

(1)求y关于x的函数解析式,并写出x的取值范围.
(2)若该商场购进这种商品的成本为9.6元/kg,则购进此商品多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系配套设计的,下表列出5套符合条件的课桌椅的高度.
椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
(1)假设课桌的高度为ycm,椅子的高度为xcm,请确定y与x的函数关系式;
(2)现有一把高38cm的椅子和一张高73.5cm的课桌,它们是否配套?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两座城市的中心火车站A,B两站相距360km.一列动车与一列特快列车分别从A,B两站同时出发相向而行,动车的平均速度比特快列车快54km/h,当动车到达B站时,特快列车恰好到达距离A站135km处的C站.则动车的平均速度是 , 特快列车的平均速度是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 图象相交于点A(﹣1,2)与点B(﹣4,n).
图象相交于点A(﹣1,2)与点B(﹣4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
(3)在第二象限内,求不等式ax+b<![]() 的解集(请直接写出答案).
的解集(请直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2= ![]() 的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=
的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC= ![]() ,点B的坐标为(m,n).
,点B的坐标为(m,n).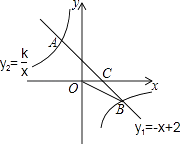
(1)求反比例函数的解析式;
(2)请直接写出当x<m时,y2的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,王老师说:“![]() 是无理数,无理数就是无限不循环小数,同学们,你能把
是无理数,无理数就是无限不循环小数,同学们,你能把![]() 的小数部分全部写出来吗?”大家议论纷纷,小刚同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用
的小数部分全部写出来吗?”大家议论纷纷,小刚同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用![]() 表示它的小数部分.”王老师说:“小刚同学的说法是正确的,因为
表示它的小数部分.”王老师说:“小刚同学的说法是正确的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.”请你解答:已知8+
的整数部分是1,将这个数减去其整数部分,差就是小数部分.”请你解答:已知8+![]() =x+y,其中x是一个整数,且0<y<1,请你求出
=x+y,其中x是一个整数,且0<y<1,请你求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=10cm,AC=8cm.点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s.当一个动点到达终点时,另一个动点也随之停止运动.设运动时间为t(s).
(1)当t为何值时,△APC为等腰三角形.
(2)当点Q在线段BC上运动时,△PBQ的面积为S(cm2),写出S与t之间的函数关系.
(3)当点Q在线段BC上运动时,是否存在某一时刻t,使S△PBQ:S四边形APQC=5:3?若存在,求出t值;若不存在,说明理由.
(4)在运动过程中,是否存在某一时刻t,使BQ平分∠ABC?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com