
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2= ![]() 的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=
的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC= ![]() ,点B的坐标为(m,n).
,点B的坐标为(m,n).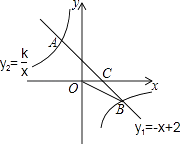
(1)求反比例函数的解析式;
(2)请直接写出当x<m时,y2的取值范围.
【答案】
(1)解:作BD⊥x轴于D,如图,
在Rt△OBD中,tan∠BOC= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,即m=﹣2n,
,即m=﹣2n,
把点B(m,n)代入y1=﹣x+2得n=﹣m+2,
∴n=2n+2,解得n=﹣2,
∴m=4,
∴B点坐标为(4,﹣2),
把B(4,﹣2)代入y2= ![]() 得k=4×(﹣2)=﹣8,
得k=4×(﹣2)=﹣8,
∴反比例函数解析式为y2=﹣ ![]()
(2)解:当0<x<4时,y2的取值范围是y2<﹣2,当x<0时,y2>0.

【解析】(1)作BD⊥x轴于D,如图,在Rt△OBD中,根据正切的定义得到tan∠BOC的值,从而m=-2n,再把点B(m,n)代入y1=-x+2得n=-m+2,然后解关于m、n的方程组得到n=-2,m=4,即B点坐标为(4,-2),再把B(4,-2)代入y2=![]() 可计算出k=-8,所以反比例函数解析式为y2=-
可计算出k=-8,所以反比例函数解析式为y2=-![]()
(2)观察函数图象得到当x<4,y2的取值范围为y2>0或y2<-2.


科目:初中数学 来源: 题型:
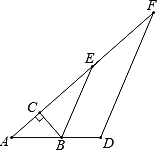
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,点F为AC延长线上的一点,连接DF.
(1)求∠CBE的度数;
(2)若∠F=25°,求证:BE∥DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于方程x2+x﹣1=0的说法中正确的是( )
A.该方程有两个相等的实数根
B.该方程有两个不相等的实数根,且它们互为相反数
C.该方程有一根为 ![]()
D.该方程有一根恰为黄金比例
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() 的角平分线与边
的角平分线与边![]() 交于点
交于点![]() ,
,![]() 的角平分线交直线
的角平分线交直线![]() 于点
于点![]() .
.
(1)若点![]() 在四边形
在四边形![]() 的内部,
的内部,
①如图,若![]() ,
,![]() ,
,![]() ,则
,则![]() _______°;
_______°;
②如图,试探索![]() 、
、![]() 、
、![]() 之间的数量关系,并将你的探索过程写下来.
之间的数量关系,并将你的探索过程写下来.
(2)如图,若点![]() 是四边形
是四边形![]() 的外部,请你直接写出
的外部,请你直接写出![]() 、
、![]() 、
、![]() 之间的数量关系.
之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,AB=3,点E在线段AB上,AE=1连结DE,DE的垂直平分线交DE于点P,交DC的延长线于点Q,PQ交BC于点G,连结EQ,EQ交BC于点F,连结GE.
(1)求证:△ADE∽△PQD;
(2)求线段CQ的长;
(3)求∠EGB的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线m与直线n相交于点O,A、B两点同时从点O出发,点A以每秒x个单位长度沿直线n向左运动,点B以每秒y个单位长度沿直线m向上运动。
(1)若运动1s时,点B比点A多运动1个单位;运动2s时,点B与点A运动的路程和为6个单位,则x=_________,y=___________.
(2)如图,当直线m与直线n垂直时,设∠BAO和∠ABO的角平分线相交于点P.在点A、B在运动的过程中,∠APB的大小是否会发生变化?若不发生变化,请求出其值(写出主要过程);若发生变化,请说明理由.
(3)如图,将(2)中的直线n不动,直线m绕点O按顺时针方向旋转α(0<ɑ<90),其他条件不变.ⅰ)用含有α的式子表示∠APB的度数____________.
ⅱ)如果再分别作△ABO的两个外角∠BAC,∠ABD的角平分线相交于点Q,并延长BP、QA交于点M.则下列结论正确的是___________(填序号) .
①APB与∠Q互补;②∠Q与∠M互余;③∠APB-∠M为定值;④∠M-∠Q为定值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)![]() 的立方根是______________.
的立方根是______________.
(2)已知某正数的两个平方根分别是a+3和2a-15,b的立方根是-2,则3a+b的算术平方根是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船沿正南方向以33海里/时的速度匀速航行,在m处观测到灯塔p在西偏南69°方向下,航行2小时后到达n处,观测灯塔p在西偏南57°方向上,若该船继续向南航行至离灯塔最近位置,求此时轮船离灯塔的距离约为多少海里?(结果精确到整数,参考数据:tan33°≈ ![]() ,sin33°≈
,sin33°≈ ![]() ,cos33°≈
,cos33°≈ ![]() ,tan21°≈
,tan21°≈ ![]() ,sin21°≈
,sin21°≈ ![]() ,c0s21°≈
,c0s21°≈ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com