
【题目】如图,已知正方形ABCD,AB=3,点E在线段AB上,AE=1连结DE,DE的垂直平分线交DE于点P,交DC的延长线于点Q,PQ交BC于点G,连结EQ,EQ交BC于点F,连结GE.
(1)求证:△ADE∽△PQD;
(2)求线段CQ的长;
(3)求∠EGB的正切值.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴DC∥AB,
∴∠AED=∠PDQ,又∠DAE=∠QPD=90°,
∴△ADE∽△PQD
(2)解:由勾股定理得,DE= ![]() =
= ![]() ,
,
∵PQ是DE的垂直平分线,
∴DP= ![]() DE=
DE= ![]() ,
,
∵△ADE∽△PQD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,DQ=5,
则CQ=DQ﹣DC=5﹣3=2
(3)解:由勾股定理得,PQ= ![]() =
= ![]() ,
,
∵∠QCG=∠QPD=90°,∠CQG=∠PQD,
∴△CQG∽△PQD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,CG= ![]() ,
,
∴BG=3﹣ ![]() =
= ![]() ,
,
∴tan∠EGB= ![]() =
= ![]()
【解析】(1)根据正方形的性质得到DC∥AB,得到∠AED=∠PDQ,根据两角对应相等的两个三角形相似证明;
(2)根据勾股定理求出DE,根据相似三角形的性质列出比例式,计算即可;
(3)根据相似三角形的性质求出CG,根据正切的概念计算即可.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】补全解答过程:
已知:如图,直线AB∥CD,直线EF与直线AB、CD分别交于点G、H,GM平分∠FGB,∠3=60°,求∠1的度数。

解:∵EF与CD交于点H(已知)
∴∠3=∠4(_______________)
∵∠3=60°(已知)
∴∠4=60°(______________)
∵AB∥CD,EF与AB、CD交于点G、H(已知)
∴∠4+∠FGB=180°(______________)
∴∠FGB=______°
∵GM平分∠FGB(已知)
∴∠1=_____°(______________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两座城市的中心火车站A,B两站相距360km.一列动车与一列特快列车分别从A,B两站同时出发相向而行,动车的平均速度比特快列车快54km/h,当动车到达B站时,特快列车恰好到达距离A站135km处的C站.则动车的平均速度是 , 特快列车的平均速度是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当三角形中一个内角是另一个内角的3倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为108°,那么这个“梦想三角形”的最小内角的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2= ![]() 的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=
的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC= ![]() ,点B的坐标为(m,n).
,点B的坐标为(m,n).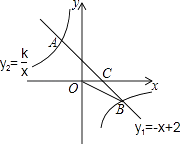
(1)求反比例函数的解析式;
(2)请直接写出当x<m时,y2的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格纸中,点A、B、C在小正方形的顶点上.
(1)求![]() 的面积;
的面积;
(2)在图中画出与![]() 关于直线1成轴对称的
关于直线1成轴对称的![]() ;
;
(3)在如图所示网格纸中,以![]() 为一边作与
为一边作与![]() 全等的三角形,可以作出多少个三角形与
全等的三角形,可以作出多少个三角形与![]() 全等(不要超出网格纸的范围).
全等(不要超出网格纸的范围).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() .
.
(1)在图中画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ;
;
(2)在图中的![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小(保留作图痕迹),并直接写出点
的值最小(保留作图痕迹),并直接写出点![]() 的坐标;
的坐标;
(3)在图中的![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小(保留作图痕迹),并直接写出
的值最小(保留作图痕迹),并直接写出![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.
(1)如图1,在等腰三角形ABC中,AB=AC,AC边上的高为h,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为h1、h2.请用面积法证明:h1+h2=h;

(2)当点M在BC延长线上时,h1、h2、h之间的等量关系式是 ;(直接写出结论不必证明)
(3)如图2在平面直角坐标系中有两条直线l1:y=![]() x+3、l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,请运用(1)、(2)的结论求出点M的坐标.
x+3、l2:y=﹣3x+3,若l2上的一点M到l1的距离是1,请运用(1)、(2)的结论求出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com