Question

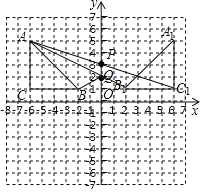
【题目】如图，在平面直角坐标系中，的三个顶点的坐标分别为，.

（1）在图中画出关于轴的对称图形；

（2）在图中的轴上找一点，使的值最小（保留作图痕迹），并直接写出点的坐标；

（3）在图中的轴上找一点，使的值最小（保留作图痕迹），并直接写出的面积.

Answer 1

【答案】（1）画图见解析；（2）画图见解析，（3）画图见解析，的面积为

【解析】

（1）根据关于y轴对称的点的坐标特征：纵坐标不变，横坐标互为相反数画图即可；（2）连接AC1交y轴于P，根据两点之间线段最短可得P即为所求，根据图象写出P点坐标即可；（3）连接AB1交y轴于Q，根据轴对称性质可得QB=QB1，所以Q点即为所求，根据S△ABQ=S△ABB1-S△QBB1即可得△ABQ的面积..

（1）如图，∵△A1B1C1与△ABC关于y轴对称，

∴A1（6，5），B1（2，1），C1（6，1），

∴△A1B1C1即为所求，

（2）如图，连接AC1，交y轴于P，点P即为所求，P（0，3）

（3）如图，连接AB1，交y轴于Q，因为BQ=QB1，所以Q即为所求，Q点坐标为（0，2）

S△ABQ=S△ABB1-S△QBB1=×4×4-×4×1=6.