
����Ŀ�������Ѿ�֪����ͨ�����㼸��ͼ�ε�������Ա�ʾһЩ�������ʽ������ͼ1���Եõ���a+b��2��a2+2ab+b2�����ڴˣ������������⣺
��1��������ͼ2��д��һ���������ʽ���� ����
��2�����ã�1���еõ��Ľ��ۣ������������⣺��a+b+c��10��ab+ac+bc��35����a2+b2+c2���� ����
��3��С��ͬѧ����ͼ3��x�ű߳�Ϊa�������Σ�y�ű߳�Ϊb�������Σ�z�ſ������ֱ�Ϊa��b�ij�����ֽƬƴ��һ�����Ϊ��2a+b����a+2b�������Σ���x+y+z���� ����
��4�������߳��ֱ�Ϊa��b��c��ֱ�������κ�һ������ֱ�DZ߶���c��ֱ��������ƴ����ͼ4�����������ͼ��ͼ�εĹ�ϵ��д��һ���������ʽ����д���Ƶ����̣�


���𰸡�(1)![]() ��(2)30��(3)9����4��
��(2)30��(3)9����4��![]()
��������
��1������ͼ2������ֱ�������ӷ��ֱ��ʾ�����������������ȷ���������ʽ��
��2�����ݣ�1���н�����������ʽ�ӵ�ֵ���ɣ�
��3��������֪��ʽ��������Ӧͼ�Σ����ɵõ����ۣ�
��4���ֱ��ʾ������ͼ�ε���������������ϵ�����ɵó����ۣ�
�⣺��1�����������ϵ�ɵã���a+b+c��2=a2+b2+c2+2ab+2ac+2bc��
��2����a+b+c=10��ab+bc+ac=35����a2+b2+c2=��a+b+c��2��2��ab+ac+bc��=100��70=30��
��3������������2a+b����a+2b��=![]() ����x=2��y=5��z=2����x+y+z=9��
����x=2��y=5��z=2����x+y+z=9��
��4��![]() �����ɣ���Ϊ����ͼ��ƴ��һ�����Σ�����
�����ɣ���Ϊ����ͼ��ƴ��һ�����Σ�����![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij������ʻ��·��S(km)��ʱ��t(min)�ĺ�����ϵͼ���۲�ͼ�����ṩ����Ϣ������������⣺
��1��������ǰ9�����ڵ�ƽ���ٶ��Ƕ��٣�
��2����������;ͣ�˶ʱ�䣿
��3����16��t��30ʱ����S��t�ĺ�����ϵʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȫ�����̣�
��֪:��ͼ��ֱ��AB��CD��ֱ��EF��ֱ��AB��CD�ֱ��ڵ�G��H��GMƽ�֡�FGB����3=60�������1�Ķ�����

��:��EF��CD���ڵ�H(��֪)
���3=��4(_______________)
�ߡ�3=60��(��֪)
���4=60��(______________)
��AB��CD��EF��AB��CD���ڵ�G��H(��֪)
���4+��FGB=180��(______________)
���FGB=______��
��GMƽ�֡�FGB(��֪)
���1=_____��(______________)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1������ƽ��ֱ������ϵ�У�A��a��0����C��b��2������C��CB��x�ᣬ�����㣨a+b��2+![]() =0��
=0��

��1����������ABC�������
��2������B��BD��AC��y����D����AE��DE�ֱ�ƽ����CAB����ODB����ͼ2������AED�Ķ�����
��3����y�����Ƿ���ڵ�P��ʹ��������ABC��������ACP�������ȣ������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о��С����������ɡ����ܱ������˶�Ա�����س������ܵ��ҵغ���ԭ·�����ܻص�أ�����˶�Ա�뿪���ص�·��s��km�����ܲ�ʱ��t��min��֮��ĺ�����ϵ��ͼ��ʾ����֪���˶�Ա�Ӽ��ܵ��ҵ�ʱ��ƽ���ٶ���0.2km/min������ͼ���ṩ����Ϣ������������⣺
��1��a=km��
��2����ί���ھ�������3km������һ�������P�����˶�Ա�ӵ�һ�ι�P�㵽�ڶ��ι�P�����õ�ʱ��Ϊ24min��
����AB����ֱ�ߵĺ�������ʽ��
�ڸ��˶�Ա����ȫ����ʱ����min��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
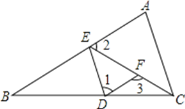
����Ŀ����ͼ����֪����A=��1����2+��3=180������BDE=65����
��1��AB��DFƽ����˵�����ɣ�
��2�����ACB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ2��������ABCD�м�ȥһ���߳�Ϊ1��С������CEFG������P�ӵ�A��������A��D��E��F��G��B��·���ƶ���εı������˶�����Bʱֹͣ��������A�͵�B�������ABP�����S����ʱ��t�仯�ĺ���ͼ������ǣ�������

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס����������е����Ļ�վA��B��վ���360km��һ�ж�����һ���ؿ��г��ֱ��A��B��վͬʱ����������У�������ƽ���ٶȱ��ؿ��г���54km/h������������Bվʱ���ؿ��г�ǡ�õ������Aվ135km����Cվ������ƽ���ٶ��� �� �ؿ��г���ƽ���ٶ��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ���������������ֱ�Ϊ
���������������ֱ�Ϊ![]() ��
��![]() .
.
��1����ͼ�л���![]() ����
����![]() ��ĶԳ�ͼ��
��ĶԳ�ͼ��![]() ��
��
��2����ͼ�е�![]() ������һ��
������һ��![]() ��ʹ
��ʹ![]() ��ֵ��С��������ͼ�ۼ�������ֱ��д����
��ֵ��С��������ͼ�ۼ�������ֱ��д����![]() �����ꣻ
�����ꣻ
��3����ͼ�е�![]() ������һ��
������һ��![]() ��ʹ
��ʹ![]() ��ֵ��С��������ͼ�ۼ�������ֱ��д��
��ֵ��С��������ͼ�ۼ�������ֱ��д��![]() �����.
�����.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com