
【题目】如图(1),在平面直角坐标系中,A(a,0),C(b,2),过C作CB⊥x轴,且满足(a+b)2+![]() =0.
=0.

(1)求三角形ABC的面积.
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
【答案】(1)4;(2)45°;(3)P点坐标为(0,3)或(0,﹣1).
【解析】
试题分析:(1)根据非负数的性质得到a=﹣b,a﹣b+4=0,解得a=﹣2,b=2,则A(﹣2,0),B(2,0),C(2,2),即可计算出三角形ABC的面积=4;
(2)由于CB∥y轴,BD∥AC,则∠CAB=∠ABD,即∠3+∠4+∠5+∠6=90°,过E作EF∥AC,则BD∥AC∥EF,然后利用角平分线的定义可得到∠3=∠4=∠1,∠5=∠6=∠2,所以∠AED=∠1+∠2=![]() ×90°=45°;
×90°=45°;
(3)先根据待定系数法确定直线AC的解析式为y=![]() x+1,则G点坐标为(0,1),然后利用S△PAC=S△APG+S△CPG进行计算.
x+1,则G点坐标为(0,1),然后利用S△PAC=S△APG+S△CPG进行计算.
解:(1)∵(a+b)2≥0,![]() ≥0,
≥0,
∴a=﹣b,a﹣b+4=0,
∴a=﹣2,b=2,
∵CB⊥AB
∴A(﹣2,0),B(2,0),C(2,2)
∴三角形ABC的面积=![]() ×4×2=4;
×4×2=4;
(2)∵CB∥y轴,BD∥AC,
∴∠CAB=∠ABD,
∴∠3+∠4+∠5+∠6=90°,
过E作EF∥AC,
∵BD∥AC,
∴BD∥AC∥EF,
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3=∠4=∠1,∠5=∠6=∠2,
∴∠AED=∠1+∠2=![]() ×90°=45°;
×90°=45°;
(3)存在.理由如下:
设P点坐标为(0,t),直线AC的解析式为y=kx+b,
把A(﹣2,0)、C(2,2)代入得![]() ,
,
解得![]() ,
,
∴直线AC的解析式为y=![]() x+1,
x+1,
∴G点坐标为(0,1),
∴S△PAC=S△APG+S△CPG=![]() |t﹣1|2+
|t﹣1|2+![]() |t﹣1|2=4,解得t=3或﹣1,
|t﹣1|2=4,解得t=3或﹣1,
∴P点坐标为(0,3)或(0,﹣1).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的个数有( )
①2是8的立方根; ②±4是64的立方根; ③无限小数都是无理数; ④带根号的数都是无理数.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字﹣2,﹣1,1,4的小球,它们的形状、大小、质地等完全相同,小强先从盒子里随机取出一个小球,记下数字为a;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为b.
(1)用列表法或画树状图表示出(a,b)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(a,b)落在二次函数y=x2的图象上的概率;
(3)求小强、小华各取一次小球所确定的数a,b满足直线y=ax+b经过一、二、三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90,D是BC的中点,E是AD的中点,过点A作AF//BC交BE的延长线于点F
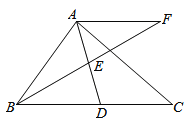
(1)求证:△AEF≌△DEB;
(2)证明:四边形ADCF是菱形;
(3)若AB=4,AC=5,求菱形ADCF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在方格中,位置如图,A点的坐标为(﹣3,1).

(1)写出B、C两点的坐标;
(2)把△ABC向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的△A1B1C1;
(3)在x轴上存在点D,使△DB1C1的面积等于3,求满足条件的点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在端午节道来之前,双十中学高中部食堂推荐了A,B,C三家粽子专卖店,对全校师生爱吃哪家店的粽子作调查,以决定最终向哪家店采购.下面的统计量中最值得关注的是( )
A. 方差 B. 平均数 C. 中位数 D. 众数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知AB∥CD,EF⊥AB于点O,∠FGC=125°,求∠EFG的度数.

下面提供三种思路:
(1)过点F作FH∥AB;
(2)延长EF交CD于M;
(3)延长GF交AB于K.
请你利用三个思路中的两个思路,
将图形补充完整,求∠EFG的度数.
解(一):
解(二):
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com