
【题目】如图,直线m与直线n相交于点O,A、B两点同时从点O出发,点A以每秒x个单位长度沿直线n向左运动,点B以每秒y个单位长度沿直线m向上运动。
(1)若运动1s时,点B比点A多运动1个单位;运动2s时,点B与点A运动的路程和为6个单位,则x=_________,y=___________.
(2)如图,当直线m与直线n垂直时,设∠BAO和∠ABO的角平分线相交于点P.在点A、B在运动的过程中,∠APB的大小是否会发生变化?若不发生变化,请求出其值(写出主要过程);若发生变化,请说明理由.
(3)如图,将(2)中的直线n不动,直线m绕点O按顺时针方向旋转α(0<ɑ<90),其他条件不变.ⅰ)用含有α的式子表示∠APB的度数____________.
ⅱ)如果再分别作△ABO的两个外角∠BAC,∠ABD的角平分线相交于点Q,并延长BP、QA交于点M.则下列结论正确的是___________(填序号) .
①APB与∠Q互补;②∠Q与∠M互余;③∠APB-∠M为定值;④∠M-∠Q为定值.

【答案】(1) 1,2.(2) ∠APB的大小不会发生变化,![]() (3)ⅰ)
(3)ⅰ) ![]() ⅱ)①②③.
ⅱ)①②③.
【解析】
(1)根据题意列出方程组,解方程即可.
(2)∠APB的大小不会发生变化,![]() 根据三角形的内角和定理得到
根据三角形的内角和定理得到![]() 根据角平分线的性质可得
根据角平分线的性质可得![]() 根据三角形的内角和定理即可求出∠APB的度数.
根据三角形的内角和定理即可求出∠APB的度数.
(3)ⅰ)参照(2)中的步骤进行求解即可.
ⅱ)分别求出∠APB,∠Q,∠M的度数,进行判断即可.
(1)根据题意可得:
![]()
解得:![]()
故答案为:1,2.
(2) ∠APB的大小不会发生变化,![]()
![]() 直线m与直线n垂直,
直线m与直线n垂直,
![]()
![]()
![]() PA,PB分别是∠BAO和∠ABO的角平分线,
PA,PB分别是∠BAO和∠ABO的角平分线,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(3)ⅰ)根据题意可得![]()
![]()
![]() PA,PB分别是∠BAO和∠ABO的角平分线,
PA,PB分别是∠BAO和∠ABO的角平分线,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
故答案为:![]()
ⅱ) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 故①∠APB与∠Q互补正确.
故①∠APB与∠Q互补正确.
![]()
![]()
![]()
![]() 故②∠Q与∠M互余正确.
故②∠Q与∠M互余正确.
![]() 是定值,故③∠APB-∠M为定值正确.
是定值,故③∠APB-∠M为定值正确.
![]() 不是定值,故④∠M-∠Q为定值错误.
不是定值,故④∠M-∠Q为定值错误.
故答案为:①②③.


科目:初中数学 来源: 题型:
【题目】如图,△ABC在正方形网格中,若A(0,3),按要求回答下列问题
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出B和C的坐标;
(3)计算△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系配套设计的,下表列出5套符合条件的课桌椅的高度.
椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
(1)假设课桌的高度为ycm,椅子的高度为xcm,请确定y与x的函数关系式;
(2)现有一把高38cm的椅子和一张高73.5cm的课桌,它们是否配套?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 图象相交于点A(﹣1,2)与点B(﹣4,n).
图象相交于点A(﹣1,2)与点B(﹣4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
(3)在第二象限内,求不等式ax+b<![]() 的解集(请直接写出答案).
的解集(请直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=﹣x+2的图象与反比例函数y2= ![]() 的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=
的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC= ![]() ,点B的坐标为(m,n).
,点B的坐标为(m,n).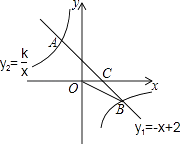
(1)求反比例函数的解析式;
(2)请直接写出当x<m时,y2的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”这批单车分为A,B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动.投放A,B两种款型的单车共100辆,总价值36800元.试问本次试点投放的A型车与B型车各多少辆?
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A,B两车型的数量比进行投放,且投资总价值不低于184万元.请问城区10万人口平均每100人至少享有A型车与B型车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,王老师说:“![]() 是无理数,无理数就是无限不循环小数,同学们,你能把
是无理数,无理数就是无限不循环小数,同学们,你能把![]() 的小数部分全部写出来吗?”大家议论纷纷,小刚同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用
的小数部分全部写出来吗?”大家议论纷纷,小刚同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用![]() 表示它的小数部分.”王老师说:“小刚同学的说法是正确的,因为
表示它的小数部分.”王老师说:“小刚同学的说法是正确的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.”请你解答:已知8+
的整数部分是1,将这个数减去其整数部分,差就是小数部分.”请你解答:已知8+![]() =x+y,其中x是一个整数,且0<y<1,请你求出
=x+y,其中x是一个整数,且0<y<1,请你求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,那么DF∥AC,请完成它成立的理由
∵∠1=∠2,∠2=∠3 ,∠1=∠4( )
∴∠3=∠4( )
∴________∥_______ ( )
∴∠C=∠ABD( )
∵∠C=∠D( )
∴∠D=∠ABD( )
∴DF∥AC( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)△EFD≌△GFB.
(2)试判断四边形FBGD的形状,并说明理由.
(3)当△ABC满足条件时,四边形FBGD是正方形(不用说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com