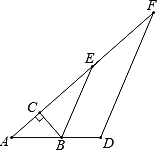
【题目】如图，在Rt△ABC中，∠ACB=90°，∠A=40°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E，点F为AC延长线上的一点，连接DF.
(1)求∠CBE的度数；
(2)若∠F=25°,求证:BE∥DF.
【答案】（1）∠CBD=65°；（2）证明见解析.
【解析】
（1）先根据直角三角形两锐角互余求出∠ABC=90°-∠A=50°，由邻补角定义得出∠CBD=130°．再根据角平分线定义即可求出∠CBE=65°；
（2）先根据三角形外角的性质得出∠CEB=90°-65°=25°，再根据∠F=25°，即可得出BE∥DF．
解：（1）∵在Rt△ABC中，∠ACB=90°，∠A=40°，
∴∠ABC=90°-∠A=50°，
∴∠CBD=130°．
∵BE是∠CBD的平分线，
∴∠CBE=
∠CBD=65°；
（2）∵∠ACB=90°，∠CBE=65°，
∴∠CEB=90°-65°=25°．
又∵∠F=25°，
∴∠F=∠CEB=25°，
∵DF∥BE．
科目：初中数学 来源： 题型：
【题目】某商场出售一批进价为2元的贺卡，在市场营销中发现此商品的日销售单价x（元）与日销售量y（个）之间有如下关系：
日销售单价x（元） | 3 | 4 | 5 | 6 |
日销售量y（个） | 20 | 15 | 12 | 10 |
（1）猜测并确定y与x之间的函数关系式，并画出图象；
（2）设经营此贺卡的销售利润为W元，求出W与x之间的函数关系式，
（3）若物价局规定此贺卡的售价最高不能超过10元/个，请你求出当日销售单价x定为多少时，才能获得最大日销售利润？最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图（1），已知：在
中，
，
，直线
经过点
，
直线，
直线，垂足分别为点
、
．证明：
．
（2）如图（2），将（1）中的条件改为：在中，，、、三点都在直线上，且
，其中
为任意锐角或钝角．请问结论是否仍然成立？如成立；请你给出证明；若不成立，请说明理由．
（3）拓展与应用：如图（3），、是直线上的两动点
、、三点互不重合），点
为
平分线上的一点，且
和
均为等边三角形，连接
、
，若
，求证：
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场欲购进一种商品，当购进这种商品至少为10kg，但不超过30kg时，成本y（元/kg）与进货量x（kg）的函数关系如图所示．
（1）求y关于x的函数解析式，并写出x的取值范围．
（2）若该商场购进这种商品的成本为9.6元/kg，则购进此商品多少千克？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】补全解答过程：
已知:如图，直线AB∥CD，直线EF与直线AB、CD分别交于点G、H，GM平分∠FGB，∠3=60°，求∠1的度数。
解:∵EF与CD交于点H(已知)
∴∠3=∠4(_______________)
∵∠3=60°(已知)
∴∠4=60°(______________)
∵AB∥CD，EF与AB、CD交于点G、H(已知)
∴∠4+∠FGB=180°(______________)
∴∠FGB=______°
∵GM平分∠FGB(已知)
∴∠1=_____°(______________)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC在正方形网格中，若A（0，3），按要求回答下列问题
（1）在图中建立正确的平面直角坐标系；
（2）根据所建立的坐标系，写出B和C的坐标；
（3）计算△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图（1），在平面直角坐标系中，A（a，0），C（b，2），过C作CB⊥x轴，且满足（a+b）2+
=0．
（1）求三角形ABC的面积．
（2）若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图2，求∠AED的度数．
（3）在y轴上是否存在点P，使得三角形ABC和三角形ACP的面积相等？若存在，求出P点坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y1=﹣x+2的图象与反比例函数y2= 
的图象相交于A，B两点，与x轴相交于点C．已知tan∠BOC= 
，点B的坐标为（m，n）．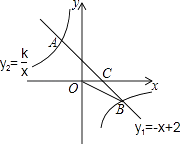
（1）求反比例函数的解析式；
（2）请直接写出当x＜m时，y2的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
