
 如图,在Rt△ABC中,∠B=90°,沿AD折叠,使点B落在斜边AC的点E处,若AB=6,BC=8,则BD=
如图,在Rt△ABC中,∠B=90°,沿AD折叠,使点B落在斜边AC的点E处,若AB=6,BC=8,则BD=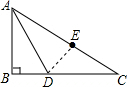 解:如图,点E是沿AD折叠,点B的对应点,连接ED,
解:如图,点E是沿AD折叠,点B的对应点,连接ED,| AB2+BC2 |


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
 将△ABC绕点C顺时针旋转90°后得到△A′B′C′,则A点的对应点A′的坐标是( )
将△ABC绕点C顺时针旋转90°后得到△A′B′C′,则A点的对应点A′的坐标是( )| A、(3,0) |
| B、(2,2) |
| C、(-3,-2) |
| D、(2,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:
 正在钓鱼岛执行保岛任务的我海监船接到情报,钓鱼岛附近有日本船只A进入我国海域.我海监船B立即出发驱赶(如图),图中l1,l2分别表示两船相对于我海监船出发地的距离s(海里)与追赶时间t(分)之间的关系.
正在钓鱼岛执行保岛任务的我海监船接到情报,钓鱼岛附近有日本船只A进入我国海域.我海监船B立即出发驱赶(如图),图中l1,l2分别表示两船相对于我海监船出发地的距离s(海里)与追赶时间t(分)之间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知AB两地相距50米,小明从A地出发去B地,以每分钟2米的速度行进,第一次他前进1米,第二次他后退2米,第三次再前进3米,第四次又向后退4米…,按此规律行进,如果A地在数轴上表示的数为-16.
已知AB两地相距50米,小明从A地出发去B地,以每分钟2米的速度行进,第一次他前进1米,第二次他后退2米,第三次再前进3米,第四次又向后退4米…,按此规律行进,如果A地在数轴上表示的数为-16.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠C=90°,AC=BC=4cm,点P从点A出发,沿AB方向以每秒
如图,在Rt△ABC中,∠C=90°,AC=BC=4cm,点P从点A出发,沿AB方向以每秒| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com