
【题目】李老师每天坚持晨跑.下图反映的是李老师某天6:20从家出发小跑到赵化北门,在北门休息几分钟后又慢跑回家的函数图象. 其中![]() (分钟)表示所用时间,
(分钟)表示所用时间, ![]() (千米)表示李欢离家的距离.
(千米)表示李欢离家的距离.
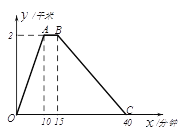
(1)分别求出线段0≤x≤10和15≤x≤40的函数解析式?
(2)李老师在这次晨跑过程中什么时间距离家500米?
【答案】(1)当0≤x≤10时,y=0.1x;当15≤x≤40时,y=3.2-0.08x;
(2)李老师在这次晨跑过程中分别于5分、33.75分距离家500米。
【解析】试题分析:(1)利用待定系数法即可求得;(2)求出OA的解析式,然后根据OA、BC的解析式,利用y=0.5千米计算求出相应的x的值,再加上6点20分即可.
试题解析:(1)设OA的解析式为y1=kx,
则10k=2,
解得k=![]() ,
,
所以,y=![]() x,
x,
设直线BC解析式为y2=k1x+b,
∵函数图象经过点(15,2),(40,0),
∴![]() ,
,
解得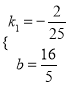 .
.
所以,直线BC解析式为y=![]() x+
x+![]() ;
;
∴线段0x10的函数解析式为y1=![]() x(0x10),
x(0x10),
线段15x40的函数解析式为y2=![]() x+
x+![]() (15x40);
(15x40);
(2)当y1=0.5km时,0.5=![]() x,x=2.5,
x,x=2.5,
当y2=0.5km时,0.5=![]() x+
x+![]() ,x=
,x=![]() =33.75,
=33.75,
∴李老师在这次晨跑过程中分别于6点22.5分和6点53.75分距离家500米。


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】2015年琼中县的槟榔产值为4200万元,2017年上升到6500万元.这两年琼中槟榔的产值平均每年增长的百分率是多少?设平均每年增长的百分率为x,根据题意列方程为( )
A. 4200(1+x)2=6500 B. 6500(1+x)2=4200
C. 6500(1﹣x)2=4200 D. 4200(1﹣x)2=6500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形ABC的周长为13cm,AB=5cm
(1)若AB是底,则AC的长为_____________cm
(2)若AB是腰,则AC的长为_____________cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点M、N在数轴上分别表示实数m,n,在数轴上M,N两点之间的距离表示为MN=m-n(m>n)或n-m(m<n)或︱m-n︱.利用数形结合思想解决下列问题:
已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
(1)点A表示的数为___________,点B表示的数为___________,点C表示的数为___________.
(2)用含t的代数式表示P到点A和点C的距离: PA= ,PC=___________.
(3)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动, Q点到达C点后,再立即以同样的速度返回,运动到终点A.
①在点Q向点C运动过程中,能否追上点P?若能,请求出点Q运动几秒追上.
②在点Q开始运动后,P、Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:函数y = (m+1) x+2 m﹣6,
(1)若函数图象过(﹣1 ,2),求此函数的解析式;
(2)若函数图象与直线 y = 2 x + 5 平行,求其函数的解析式;
(3)求满足②条件的直线与此同时y =﹣3 x + 1 的交点。
查看答案和解析>>
科目:初中数学 来源: 题型:
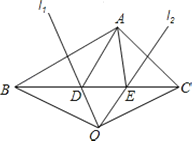
【题目】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接0B,OC,若△ADE的周长为6cm,△OBC的周长为16cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=120°,求∠DAE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com