
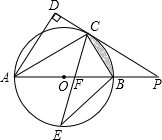
 ��ͼ��AB�ǡ�O��ֱ������C�ǡ�O��һ�㣬AD�����C�����ߴ�ֱ������ΪD��ֱ��DC��AB���ӳ��߽��ڵ�P����CEƽ�֡�ACB����AB�ڵ�F������BE��BE=7$\sqrt{2}$�������ĸ����ۣ���ACƽ�֡�DAB����PF2=PB•PA������BC=$\frac{1}{2}$OP������Ӱ���ֵ����Ϊ$\frac{7}{4}$��-$\frac{49}{4}$$\sqrt{3}$������PC=24����tan��PCB=$\frac{3}{4}$��������ȷ���ǣ�������
��ͼ��AB�ǡ�O��ֱ������C�ǡ�O��һ�㣬AD�����C�����ߴ�ֱ������ΪD��ֱ��DC��AB���ӳ��߽��ڵ�P����CEƽ�֡�ACB����AB�ڵ�F������BE��BE=7$\sqrt{2}$�������ĸ����ۣ���ACƽ�֡�DAB����PF2=PB•PA������BC=$\frac{1}{2}$OP������Ӱ���ֵ����Ϊ$\frac{7}{4}$��-$\frac{49}{4}$$\sqrt{3}$������PC=24����tan��PCB=$\frac{3}{4}$��������ȷ���ǣ�������| A�� | �٢� | B�� | �ۢ� | C�� | �٢ڢ� | D�� | �٢ڢ� |
���� ������OC���������ߵ����ʿɵ�OC��CD����AD��OC�����ݵȱ߶ԵȽǣ��Լ�ƽ���ߵ����ʼ���֤�ã�
�ڸ���Բ�ܽǶ����Լ������ε���ǵ����ʶ���֤����PFC=��PCF�����ݵȽǶԵȱ���֤��PC=PF�����ɡ�PCB=��PAC����P=��P����֤�á�PCB�ס�PAC��Ȼ�������������εĶ�Ӧ�߳ɱ�����֤�ý��ۣ�
����������AE����Բ�ܽǶ�������CEƽ�֡�ACB���ɵá�ABE�ǵ���ֱ�������Σ��̶����ֱ��AB�ij�����BC=$\frac{1}{2}$OP���ɵ�BC�����ߣ���OBC�ǵȱ������Σ��̶������Ӱ���ֵ������
����ֱ�ǡ�POC�����ù��ɶ��������з������PB�ij����ɡ�PCB�ס�PAC���������������ε��������PB��PC�ı�ֵ���������tan��PCB��
��� �⣺������OC��
��OA=OC��
���OAC=��OCA��
��PC�ǡ�O�����ߣ�AD��CD��
���OCP=��D=90�㣬
��OC��AD��
���CAD=��OCA=��OAC��
��ACƽ�֡�DAB������ȷ��
�ڡ�AB��ֱ����
���ACB=90�㣬
���PCB+��ACD=90�㣬
�֡ߡ�CAD+��ACD=90�㣬
���CAB=��CAD=��PCB��
�֡ߡ�ACE=��BCE����PFC=��CAB+��ACE����PCF=��PCB+��BCE��
���PFC=��PCF��
��PC=PF��
�ߡ�P�ǹ����ǣ�
���PCB�ס�PAC��
��PC��PA=PB��PC��
��PC2=PB•PA��
��PF2=PB•PA������ȷ��
��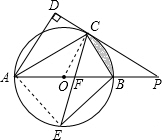 ����AE��
����AE��
�ߡ�ACE=��BCE��
��$\widehat{AE}$=$\widehat{BE}$��
��AE=BE��
�֡�AB��ֱ����
���AEB=90�㣮
��AB=$\sqrt{2}$BE=$\sqrt{2}$��7$\sqrt{2}$=14��
��OB=OC=7��
��PD�����ߣ�
���OCP=90�㣬
��BC=$\frac{1}{2}$OP��
��BC��Rt��OCP�����ߣ�
��BC=OB=OC��
����OBC�ǵȱ������Σ�
���BOC=60�㣬
��S��BOC=$\frac{49}{4}$$\sqrt{3}$��S����BOC=$\frac{60}{360}$����72=$\frac{49}{6}$��
����Ӱ���ֵ����Ϊ$\frac{49}{6}$��-$\frac{49}{4}$$\sqrt{3}$���ʴ���
�ܡߡ�PCB�ס�PAC��
��$\frac{PB}{PC}=\frac{BC}{AC}$��
��tan��PCB=tan��PAC=$\frac{BC}{AC}$=$\frac{PB}{PC}$��
��PB=x����PA=x+14��
��PC2=PB•PA��
��242=x��x+14����
��ã�x1=18��x2=-32��
��PB=18��
��tan��PCB=$\frac{PB}{PC}$=$\frac{18}{24}$=$\frac{3}{4}$������ȷ��
��ѡC��
���� ��������Բ���ۺ��⣬������Բ�����������Լ���ֱ�������ε�֪ʶ���������ߵ����������м������֤����ͨ��������������Բ�ĺ��е㣬���ô�ֱ����ֱ�������ν���й����⣮


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | ��-3 | C�� | 0.3 | D�� | -$\sqrt{1.2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
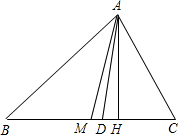 ��ͼ��AD��AM��AH�ֱ��ABC�Ľ�ƽ���ߡ����ߺߣ�����ͼ�Σ�д��������ͬ����ȹ�ϵʽAH��AB��AH��AD��AH��AM��
��ͼ��AD��AM��AH�ֱ��ABC�Ľ�ƽ���ߡ����ߺߣ�����ͼ�Σ�д��������ͬ����ȹ�ϵʽAH��AB��AH��AD��AH��AM���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com