
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
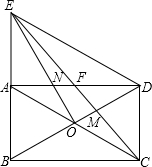 如图,矩形ABCD的对角线交于O点,已知∠ABD=60°,过点O作EO⊥BD交BA延长线于点E,交AD于点N,连接ED、EC,EC分别交AD、BD于点F和点M.
如图,矩形ABCD的对角线交于O点,已知∠ABD=60°,过点O作EO⊥BD交BA延长线于点E,交AD于点N,连接ED、EC,EC分别交AD、BD于点F和点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:正方形OABC的顶点O在坐标原点,点A的坐标为(12,5).
如图:正方形OABC的顶点O在坐标原点,点A的坐标为(12,5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
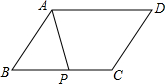 如图,在平行四边形ABCD中,点P是BC边的中点,设$\overrightarrow{CD}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b$,
如图,在平行四边形ABCD中,点P是BC边的中点,设$\overrightarrow{CD}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b$,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
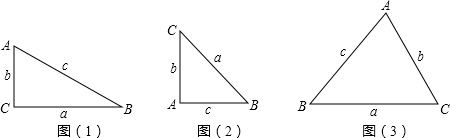 发现问题:
发现问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.
为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.| 进球数(个) | 人数 |
| 0 | 1 |
| 1 | 2 |
| 2 | x |
| 3 | y |
| 4 | 4 |
| 5 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com